Χαρτογράφηση του Χωρόχρονου
Μέρος 08
Τα σχήματα
που συνθέτουν το σχήμα του Χωρόχρονου
που συνθέτουν το σχήμα του Χωρόχρονου
Τελειώνοντας το 7ο μέρος δηλώσαμε ότι υπάρχουν σχήματα που συμπεριφέρονται ως "μοναδιαία" όλα τα υπάρχοντα κανονικά σχήματα αποτελούν συνδυασμούς και τροποποιήσεις τους και γενικών προκύπτουν από αυτά.
(όπως ακριβώς, από τα βασικά χρώματα προκύπτουν με μίξη όλες οι υπόλοιπες αποχρώσεις)
Είναι τα λεγόμενα "κωνοειδή" ή κωνικές τομές.
Πρώτοι οι Αρχαίοι Έλληνες Μαθηματικοί τα εντόπισαν αλλά δεν μπορούσαν, βέβαια, να αντιληφθούν τον θεμελιακό ρόλο τους.
Αυτά δεν είναι αυθαίρετα.
Είναι λύσεις της πλέον κομψής και συμμετρικής αλγεβρικής εξίσωσης της Άλγεβρας.
Είναι αυτή που ονομάζεται "Τρισδιάστατη Δευτεροβάθμια Ομογενής Γραμμική Αλγεβρική Εξίσωση"
Είναι λύσεις της πλέον κομψής και συμμετρικής αλγεβρικής εξίσωσης της Άλγεβρας.
Είναι αυτή που ονομάζεται "Τρισδιάστατη Δευτεροβάθμια Ομογενής Γραμμική Αλγεβρική Εξίσωση"
 |
| όπου, κάποιος από τους συντελεστές α θα είναι πάντοτε διάφορος του μηδενός |
Ακολουθεί ο πίνακας με τα 24 αυτά σχήματα (18 θεμελιώδη + 6 παράγωγα) τοποθετημένα ανά τριάδες.
--------------
| A. Κωνοειδή 1ης τριάδας | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
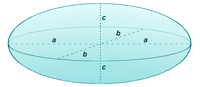
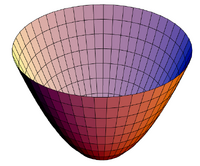
| A1. | Πραγματικό Ελλειψοειδές |  | |
| A2. | Ελλειπτικός Κύλινδρος |  | |
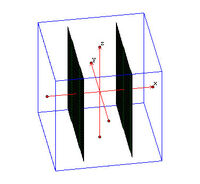
| A3. | Ζεύγος Πραγματικών Παραλλήλων Επιπέδων |  | |
| B. Κωνοειδή 2ης τριάδας (Υπερβολικοειδή) | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
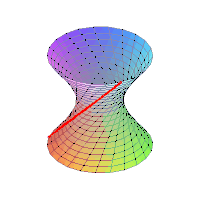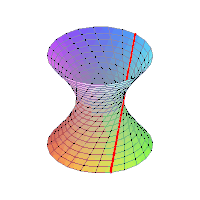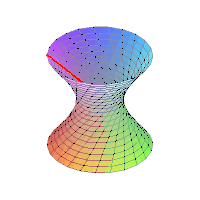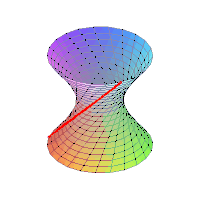
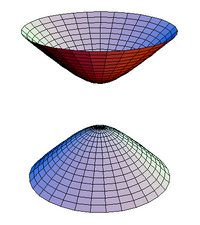
| B1. | Μονόχωνο Υπερβολοειδές |  | |
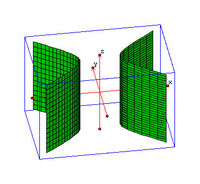
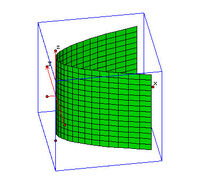
| B2. | Υπερβολικός Κύλινδρος |  | |
| B3. | Ζεύγος Πραγματικών Παραλλήλων Επιπέδων (Ταυτίζεται με το A3) |  | |
| C. Κωνοειδή 3ης τριάδας (Ελλειψικοειδή) | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
| C1. | Φανταστικό Ελλειψοειδές |  | Μη Υπαρκτό Γεωμετρικό Σχήμα ( = Δεν μπορεί να σχεδιασθεί στον "Κόσμο μας") |
| C2. | Φανταστικός Κύλινδρος |  | Μη Υπαρκτό Γεωμετρικό Σχήμα ( = Δεν μπορεί να σχεδιασθεί στον "Κόσμο μας") |
| C3. | Ζεύγος Φανταστικών Παραλλήλων Επιπέδων |  | Μη Υπαρκτό Γεωμετρικό Σχήμα ( = Δεν μπορεί να σχεδιασθεί στον "Κόσμο μας") |
| D. Κωνοειδή 4ης τριάδας (Υπερβολικοειδή) | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
| D1. | Δίχωνο Υπερβολοειδές |  | |
| D2. | Υπερβολικός Κύλινδρος(Ταυτίζεται με το Β2) |  | |
| D3. | Ζεύγος Φανταστικών Παραλλήλων Επιπέδων (Ταυτίζεται με το C3) |  | Μη Υπαρκτό Γεωμετρικό Σχήμα ( = Δεν μπορεί να σχεδιασθεί στον "Κόσμο μας") |
| E. Κωνοειδή 5ης τριάδας (Κωνικοειδή) | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
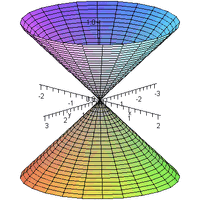
| E1. | Ελλειπτικός Κώνος |  | Μη Ολοκληρωμένο Γεωμετρικό Σχήμα ( = Μόνο ένα σημείο του (η κορυφή του) μπορεί να σχεδιασθεί στον "Κόσμο μας") |
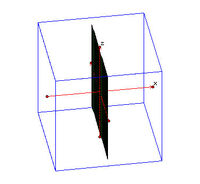
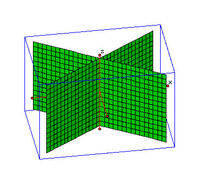
| E2. | Ζεύγος Φανταστικών Τεμνομένων Επιπέδων |  | Μη Ολοκληρωμένο Γεωμετρικό Σχήμα ( = Μόνο μία ευθεία τους (η τομή τους) μπορεί να σχεδιασθεί στον "Κόσμο μας") |
| E3. | Ζεύγος Πραγματικών Συμπιπτόντων Επιπέδων |  | |
| F. Κωνοειδή 6ης τριάδας (Παραβολικοειδή) ***Μη θεμελιώδη*** | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
| F1. | Ελλειπτικό Παραβολοειδές |  | |
| F2. | Παραβολικός Κύλινδρος |  | |
| F3. | Ζεύγος Πραγματικών Συμπιπτόντων Επιπέδων(ταυτίζεται με το E3) |  | |
| G. Κωνοειδή 7ης τριάδας (Κωνικοειδή) | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
| G1. | Υπερβολικός Κώνος |  | |
| G2. | Ζεύγος Πραγματικών Τεμνομένων Επιπέδων |  | |
| G3. | Ζεύγος Πραγματικών Συμπιπτόντων Επιπέδων (ταυτίζεται με το E3) |  | |
| H. Κωνοειδή 8ης τριάδας (Παραβολικοειδή) ***Μη θεμελιώδη*** | |||
|---|---|---|---|
| α/α | Ονομασία | Αλγεβρική Αναπαράσταση | Γεωμετρική Αναπαράσταση |
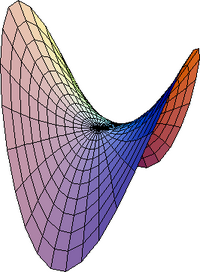
| H1. | Υπερβολικό Παραβολοειδές |  | |
| H2. | Παραβολικός Κύλινδρος |  | |
| H3. | Ζεύγος Πραγματικών Συμπιπτόντων Επιπέδων (ταυτίζεται με το F3) |  | |
--------------

 Added by
Added by 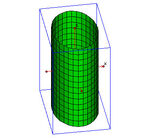

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου