Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο19-
Αναζήτηση
"κρυμμένων" Διαστάσεων
"κρυμμένων" Διαστάσεων
--------------------------------------------------------------------
--------------------------------------------------------------------
Στο προηγούμενο ολοκληρώθηκε το πρώτο μέρος της Εισαγωγής
που άρχισε στο μέρος.
Ακολουθεί, λοιπόν, το δεύτερο μέρος.
Συνεχίζουμε λοιπόν την επέκταση του Χωρόχρονου...
- Για στάσου, ρε Ionn, εσύ δεν μας είπες στο προηγούμενο ότι
ο Χωρόχρονος AdS είναι το τελειότερο και
απόλυτα πλήρες μοντέλο Μαθηματικού Χώρου
που δημιούργησε ο Άνθρωπος,
μετά από σκληρή επεξεργασία 5000 χιλιάδων ετών περίπου,
και που ανταποκρίνεται απόλυτα
σε ότι θεωρούμε ότι είναι ο Χωρόχρονος της Φύσης???
- Ναι, το είπα.
- Τότε που κολλάει το "συνεχίζουμε"?
- Θα προσπαθήσω να το εξηγήσω
Αν στην Φύση, η Ύλη υπήρχαν μόνο Σωματίδια και Σώματα
τότε ο Χωρόχρονος AdS θα μας κάλυπτε πλήρως
- Αλλά?
- Αλλά υπάρχουν και τα Κύματα
- Δηλαδή?
- Δηλαδή, μουσική, χρώματα, ραδιοφωνικά και τηλεοπτικά σήματα,
με άλλα λόγια, Ηλεκτρομαγνητική Ακτινοβολία
- Ε, και λοιπόν? Δεν τα βλέπουμε τα Κύματα?
- Τα μισο-βλέπουμε?
- Μα τι λες τώρα? Πέτα μια πέτρα σε μια λίμνη και δες τα.
Δεν τα βλέπεις ολόκληρα? Τι μας λες ότι τα "μισο-βλέπεις"?
Λοιπόν, τα Κύματα είναι ένα από τα πολλά επαναλαμβανόμενα φαινόμενα
της Φύσης. Οτιδήποτε περιέχει επανάληψη
θα μπορούσαμε να πούμε ότι το βλέπουμε "περιληπτικά".
Ας ξεκινήσουμε, λοιπόν, εντελώς απλά.
Ας δούμε το απλούστερο παράδειγμα επαναλαμβανόμενου φαινομένου
δηλ. την Απλή Ταλάντωση του Ελατηρίου.
Ας δούμε τις κύριες θέσεις του "παγωμένες" (δηλ. χωρίς να κυλά ο Χρόνος)
Για καλύτερη "οπτική εικόνα" του θέματος κάποιοι φυσικοί
(μεταξύ αυτών και ο Joseph-Louis Lagrange)
σκέφτηκαν να παρατηρήσουν αυτό το επαναλαμβανόμενο φαινόμενο
(και κατά συνέπεια, και όλα τα Περιοδικά Φαινόμενα)
από ένα νέο Σύστημα Συντεταγμένων
που θα περιείχε άλλη μία "διάσταση". Ποιά???
Μα .... την ταχύτητα (v).
Ουσιαστικά, είχαμε "συγκόλληση" στον 1D-Πραγματικό Χώρο
ενός αντίστοιχου 1D-Φασματικού Χώρου
Το αποτέλεσμα της συγκόλλησης αυτής ονομάσθηκε Φασικός Χώρος (Phase space)
ή Χώρος Διαμόρφωσης (configuration space)
Βέβαια, στο παραπάνω παράδειγμα
παρουσιάστηκε μία κίνηση
στο 1D-Πραγματικό Χώρο, με μία διάσταση (x)
που απαίτησε μία ταχύτητα (v)
Προφανώς, αυτά επεκτείνονται
στον 3D-Πραγματικό Χώρο, με τρείς διαστάσεις (x,y,z)
οπότε απαιτούνται, αντίστοιχα, και τρεις ταχύτητες
Επομένως, ο αντίστοιχος Φασικός Χώρος θα έχει (3+3 =) 6 "διαστάσεις".
Ο Φασματικός Χώρος των ταχυτήτων ποτέ δεν θεωρήθηκε, βέβαια,
ως κάποια προέκταση του Πραγματικού Χώρου
αλλά απλή "αναπαράσταση", δηλ. ένα μαθηματικό εργαλείο
για την καλύτερη κατανόηση των φυσικών φαινομένων.
Στο προηγούμενο ολοκληρώθηκε το πρώτο μέρος της Εισαγωγής
που άρχισε στο μέρος.
Ακολουθεί, λοιπόν, το δεύτερο μέρος.
 |
| Ούς, η Βιολογική Ακουστική Συσκευή που χωρίς να "διαβλέπει" καθαυτόν τον Φασικό Χώρο άνοιξε τον δρόμο στην ανακάλυψή του καθώς προσλαμβάνει τα Ηχητικά Κύματα τα οποία οποία εξαπλώνονται ταυτόχρονα εκτός από τον 3D-Ευκλείδειο χώρο και στον 3D-Φασματικό |
Συνεχίζουμε λοιπόν την επέκταση του Χωρόχρονου...
- Για στάσου, ρε Ionn, εσύ δεν μας είπες στο προηγούμενο ότι
ο Χωρόχρονος AdS είναι το τελειότερο και
απόλυτα πλήρες μοντέλο Μαθηματικού Χώρου
που δημιούργησε ο Άνθρωπος,
μετά από σκληρή επεξεργασία 5000 χιλιάδων ετών περίπου,
και που ανταποκρίνεται απόλυτα
σε ότι θεωρούμε ότι είναι ο Χωρόχρονος της Φύσης???
- Ναι, το είπα.
- Τότε που κολλάει το "συνεχίζουμε"?
- Θα προσπαθήσω να το εξηγήσω
Αν στην Φύση, η Ύλη υπήρχαν μόνο Σωματίδια και Σώματα
τότε ο Χωρόχρονος AdS θα μας κάλυπτε πλήρως
- Αλλά?
- Αλλά υπάρχουν και τα Κύματα
- Δηλαδή?
- Δηλαδή, μουσική, χρώματα, ραδιοφωνικά και τηλεοπτικά σήματα,
με άλλα λόγια, Ηλεκτρομαγνητική Ακτινοβολία
- Ε, και λοιπόν? Δεν τα βλέπουμε τα Κύματα?
- Τα μισο-βλέπουμε?
- Μα τι λες τώρα? Πέτα μια πέτρα σε μια λίμνη και δες τα.
Δεν τα βλέπεις ολόκληρα? Τι μας λες ότι τα "μισο-βλέπεις"?
 |
| Κύματα επιφάνειας λίμνης (δηλ. σε 2D-Χώρο) (σχηματίζουν "όρη" και "κοιλάδες") |
της Φύσης. Οτιδήποτε περιέχει επανάληψη
θα μπορούσαμε να πούμε ότι το βλέπουμε "περιληπτικά".
Ας ξεκινήσουμε, λοιπόν, εντελώς απλά.
Ας δούμε το απλούστερο παράδειγμα επαναλαμβανόμενου φαινομένου
δηλ. την Απλή Ταλάντωση του Ελατηρίου.
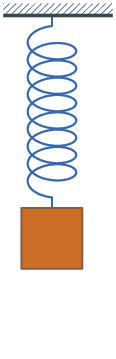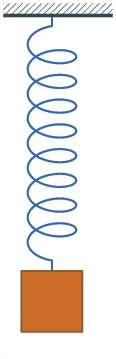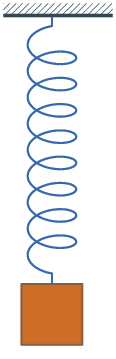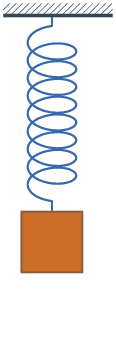 |
| Ένα ελατήριο κινείται σε μία ευθεία δηλ. σε ένα μονοδιάστατο 1D- Χώρο (εφόσον θεωρήσουμε αμελητέο το μέγεθός του αλλιώς 2D ή 3D- Χώρο) |
Ας δούμε τις κύριες θέσεις του "παγωμένες" (δηλ. χωρίς να κυλά ο Χρόνος)
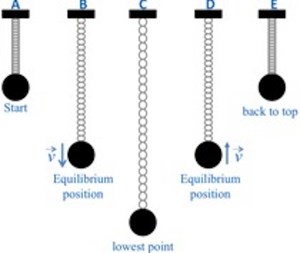 |
| Παρατηρούμε τριών ειδών θέσεις στην ταλάντωση του ελατήριου - την άνω ακραία (top) - την μεσαία (equilibriuum) (ή θέση ισορροπίας) - την κάτω ακραία (lowest) ---- - Στις ακραίες θέσεις η ταχύτητα (v) μηδενίζεται (για να γίνει η αντιστροφή κίνησης) ενώ η απόσταση (x) από την ισορροπία γίνεται μέγιστη. - Αντίθετα, στις μεσαίες η ταχύτητα (v) γίνεται μέγιστη και η απόσταση (x) μηδενίζεται (καθώς εκεί τοποθετούμε την αρχή της μέτρησης) |
Για καλύτερη "οπτική εικόνα" του θέματος κάποιοι φυσικοί
(μεταξύ αυτών και ο Joseph-Louis Lagrange)
σκέφτηκαν να παρατηρήσουν αυτό το επαναλαμβανόμενο φαινόμενο
(και κατά συνέπεια, και όλα τα Περιοδικά Φαινόμενα)
από ένα νέο Σύστημα Συντεταγμένων
που θα περιείχε άλλη μία "διάσταση". Ποιά???
Μα .... την ταχύτητα (v).
Ουσιαστικά, είχαμε "συγκόλληση" στον 1D-Πραγματικό Χώρο
ενός αντίστοιχου 1D-Φασματικού Χώρου
Το αποτέλεσμα της συγκόλλησης αυτής ονομάσθηκε Φασικός Χώρος (Phase space)
ή Χώρος Διαμόρφωσης (configuration space)
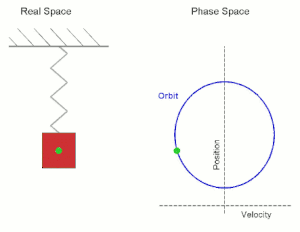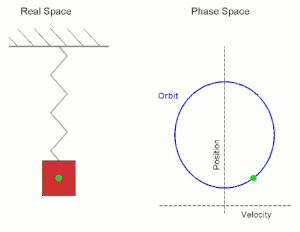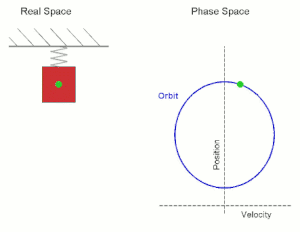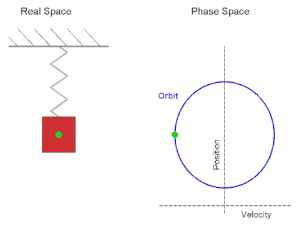 |
| Αναπαραστάσεις της ταλάντωσης του ελατήριου - Αριστερά: στον 1D-Πραγματικό Χώρο (1 άξονας = απόσταση (position) (x)) - Δεξιά: στον (1,1)D-Φασικό Χώρο (2 άξονες = απόσταση (position) (x) + ταχύτητα (velocity) (v)) ---- Η πράσινη τελεία είναι το κέντρο βάρους του σώματος Στον (1,1)D-Φασικό Χώρο το σχήμα του σώματος είναι πολύ διαφορετικό και πολύ δύσκολο να αναπαρασταθεί όμως, έτσι κι αλλιώς, ενδιαφερόμαστε μόνο για την κίνηση του κέντρου βάρους του δηλ. της πράσινης τελείας. |
Βέβαια, στο παραπάνω παράδειγμα
παρουσιάστηκε μία κίνηση
στο 1D-Πραγματικό Χώρο, με μία διάσταση (x)
που απαίτησε μία ταχύτητα (v)
Προφανώς, αυτά επεκτείνονται
στον 3D-Πραγματικό Χώρο, με τρείς διαστάσεις (x,y,z)
 |
| Προσθήκη λεζάντας |
οπότε απαιτούνται, αντίστοιχα, και τρεις ταχύτητες
 |
| Προσθήκη λεζάντας |
Η νέα αυτή "οπτική γωνία" (ορθότερα, αναπαράσταση) της Περιοδικής Κίνησης
δημιούργησε έναν νέο κλάδο της Κλασσικής Μηχανικής
(εκτός της μόνης, μέχρι τότε, γνωστής Μηχανικής του Νεύτωνα):
την Αναλυτική Μηχανική Lagrange (θεμελίωση το 1788)
δημιούργησε έναν νέο κλάδο της Κλασσικής Μηχανικής
(εκτός της μόνης, μέχρι τότε, γνωστής Μηχανικής του Νεύτωνα):
την Αναλυτική Μηχανική Lagrange (θεμελίωση το 1788)
 |
| Joseh-Louis Langrange (1736 - 1813) Διαπρεπής Ιταλός φυσικός "Πατέρας" της Αναλυτικής Μηχανικής --- Ποτέ δεν φαντάστηκε ότι, μάλλον, στο μέλλον θα θεωρηθεί και ως "πάππος" της Χορδοθεωρίας και της Πολυδιαστατικής Φυσικής |
ως κάποια προέκταση του Πραγματικού Χώρου
αλλά απλή "αναπαράσταση", δηλ. ένα μαθηματικό εργαλείο
για την καλύτερη κατανόηση των φυσικών φαινομένων.
-------------------------------------------------------------------
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου