IonnKorr: Electromagnetism a la Mendeleev

Κυριακή 4 Σεπτεμβρίου 2016

Electromagnetism a la Mendeleev - A-02

Ηλεκτρομαγνητισμός αλά Mendeleev
-A-02-

Υπερβολή

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στο προηγούμενο μέρος ξεκινήσαμε από έναν δισ-διάστατο 2D-Χώρο
και μελετήσαμε, μία θεμελιώδη καμπύλη, την Έλλειψη
(που είναι, απλά, ένας γενικευμένος Κύκλος)

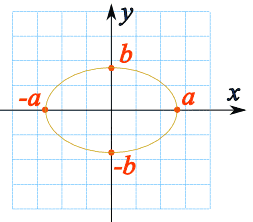Στο σχήμα βλέπουμε
ότι
α = το σημείο που η Έλλειψη τέμνει την Διάσταση (x)
b = το σημείο που η Έλλειψη τέμνει την Διάσταση (y)

Η εξίσωση που περιγράφει την Έλλειψη, στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Παρατηρούμε ότι
και οι δύο όροι που περιέχουν τους άξονες
είναι θετικοί (+)

Συνεχίζουμε τώρα με μία άλλη θεμελιώδη καμπύλη, την Υπερβολή.

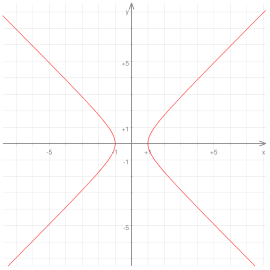Στο σχήμα παρατηρούμε
ότι η Υπερβολή
τέμνει μόνον τον άξονα x (σε δύο σημεία)
αλλά δεν τέμνει σε κανένα σημείο τον άξονα y.

Η εξίσωση που περιγράφει την Υπερβολή, στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Παρατηρούμε ότι η διαφορά
με την εξίσωση που περιγράφει την Έλλειψη
είναι το σημείο "μείον" (-)
του όρου που περιέχει τον άξονα y
δεν τέμνει την καμπύλη

------
Συνεχίζουμε τώρα με την μελέτη των δύο αυτών θεμελιωδών καμπυλών
από την σκοπιά της Πολυδιαστατικής Θεωρίας
(δηλ. από την σκοπιά του Ενιαίου 11D-Χωρόχρονου)

Όπως είδαμε στο προηγούμενο μέρος, η εξίσωση της Έλλειψης
από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Red}y^{2}}{\color {Red}b^{2}}}=1$

Υπενθυμίζουμε ότι οι ερυθρές Διαστάσεις (x, y, z) είναι
οι συνήθεις γνωστές πραγματικές διαστάσεις
(του Πραγματικού Χώρου της Υπαρκτής Πραγματικότητας).
Αυτές, λοιπόν, (όπως τις κατανοεί ο Χορδιακός Παρατηρητής)
διαθέτουν την ιδιότητα της έλξης
(μία ιδιότητα που η Κλασσική Φυσική
αποδίδει στα Θεμελιώδη Πεδία).
Δηλαδή, έλκουν τα άκρα μίας Υλικής Καμπύλης
("χορδής" σύμφωνα με την Χορδοθεωρία)
και την αναγκάζουν να τμήσει
τους αντίστοιχους άξονες.

Τώρα, η εξίσωση της Υπερβολής
από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Blue}y^{2}}{\color {Blue}b^{2}}}=1$

[Η εξίσωση αυτή προκύπτει από την κλασσική της μορφή
με χρήση της ταυτότητας i²= -1 οπότε -y²= y²]

Υπενθυμίζουμε ότι οι καστανόχροες Διαστάσεις (x, y, z) είναι
οι πρόσθετες φανταστικές διαστάσεις
(του 11D-Χωρόχρονου).
Αυτές, λοιπόν, (όπως τις κατανοεί ο Χορδιακός Παρατηρητής)
διαθέτουν την ιδιότητα της άπωσης
(επίσης, μία ιδιότητα που η Κλασσική Φυσική
αποδίδει στα Θεμελιώδη Πεδία).
Δηλαδή, απωθούν τα άκρα μίας Υλικής Καμπύλης
("χορδής" σύμφωνα με την Χορδοθεωρία)
και την αναγκάζουν να μην τμήσει
τους αντίστοιχους άξονες.

-------------
Ωραία όλα αυτά.
Όμως, θα τα μπορούσε να θεωρήσει, κάποιος, εντελώς φορμαλιστικά
Δηλαδή, μία θέαση απόλυτα ισοδύναμη με την κλασσική.
Όμως....
όπως θα δούμε στα επόμενα
είναι απλά η κορυφή ενός τεράστιου παγόβουνου
και πίσω της κρύβεται ένας ολοκαίνουργιος, άγνωστος, εξωτικός κόσμος.

--------------------------------

ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:

${\vec {r}}={\begin{bmatrix}\color {pink}{q}\\\color {Red}{x}\\\color {Red}{y}\\\color {Red}{z}\\\color {pink}{t}\\e\\\color {cyan}{t}\\\color {blue}{z}\\\color {blue}{y}\\\color {blue}{x}\\\color {cyan}{q}\end{bmatrix}}$

Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου:
το ροδόχροο (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου
τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου
το ροδόχροο (t) = η Διάσταση του Πραγματικού Χρόνου
το μαύρο (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου

το κυανό (t) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος)
τα γλαυκά (z, y, x) οι Διαστάσεις του Φανταστικού Χώρου
(ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος)
το κκυανό (q) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------