Ηλεκτρομαγνητισμός αλά Mendeleev
-A-03-
--------------------------------------------------------------------
--------------------------------------------------------------------
Το είχαμε αναφέρει και παλαιότερα
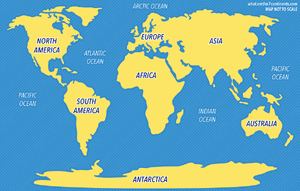
Παρατηρώντας, τον συνήθη χάρτη της Γης,
δεν μπορούμε να αποφύγουμε την απορία.
Γιατί να έχουν αυτό το σχήμα οι Ήπειροι?
Η Κλασσική Γεωλογία απαντούσε, για αιώνες, επιγραμματικά:
- Έτσι τις σχημάτισε η Φύση (ή εναλλακτικά, ο Θεός)
Όμως...
ήρθε η "τεκτονική" Γεωλογία
και εξήγησε το θεωρούμενο ως παντελώς ανεξήγητο σχήμα
Οι Ήπειροι δεν είναι χρονικά αναλλοίωτοι.
Ακολούθησαν, και αυτές, μία τεράστια Εξελικτική πορεία
ανάλογη με των Βιολογικών Όντων του Πλανήτη.
Έτσι π.χ. ανακαλύφθηκε ότι
στο Νότιο Ημισφαίριο
υπήρχε μία τεράστια αρχαιοήπειρος, η Γονδοβάνη (Gondwana)
που λόγω τεράστιων μετακινήσεων
των τεκτονικών πλακών του Φλοιού της Γης
έσπασε σε μικρότερα τμήματα.
Αν λοιπόν ήταν λογικό και εποικοδομητικό
να αναρωτηθούμε για το σχήμα των αντικειμένων της Γεωλογίας
γιατί να είναι παράλογο
να αναρωτηθούμε για το σχήμα των αντικειμένων της Γεωμετρίας???
Ας σημειωθεί ότι οι δύο αυτές Καμπύλες (Έλλειψη και Υπερβολή)
είναι τόσο θεμελιώδεις στην Γεωμετρία
όσο και οι Ήπειροι στην Γεωγραφία
(Όλες οι καμπύλες της Γεωμετρίας παράγονται από αυτές τις δύο
καθώς και μερικές άλλες που θα αναφέρουμε αργότερα
Θα μπορούσαμε να τις αντιστοιχήσουμε με τους 10 αριθμούς
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
του Δεκαδικού Συστήματος της Αριθμητικής
από τους οποίους παράγονται όλοι οι άπειροι υπόλοιποι αριθμοί)
Ας το ψάξουμε λοιπόν.
-----
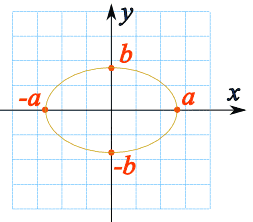
Ας ξαναδούμε το σχήματα της Έλλειψης και της Υπερβολής.
- Το πρώτο, της Έλλειψης
είναι ενιαίο, ευλογοφανές, αρμονικό, τέλειο.
Το είχαμε αναφέρει και παλαιότερα

Παρατηρώντας, τον συνήθη χάρτη της Γης,
δεν μπορούμε να αποφύγουμε την απορία.
Γιατί να έχουν αυτό το σχήμα οι Ήπειροι?
Η Κλασσική Γεωλογία απαντούσε, για αιώνες, επιγραμματικά:
- Έτσι τις σχημάτισε η Φύση (ή εναλλακτικά, ο Θεός)
Όμως...
ήρθε η "τεκτονική" Γεωλογία
και εξήγησε το θεωρούμενο ως παντελώς ανεξήγητο σχήμα
Οι Ήπειροι δεν είναι χρονικά αναλλοίωτοι.
Ακολούθησαν, και αυτές, μία τεράστια Εξελικτική πορεία
ανάλογη με των Βιολογικών Όντων του Πλανήτη.
Έτσι π.χ. ανακαλύφθηκε ότι
στο Νότιο Ημισφαίριο
υπήρχε μία τεράστια αρχαιοήπειρος, η Γονδοβάνη (Gondwana)
που λόγω τεράστιων μετακινήσεων
των τεκτονικών πλακών του Φλοιού της Γης
έσπασε σε μικρότερα τμήματα.
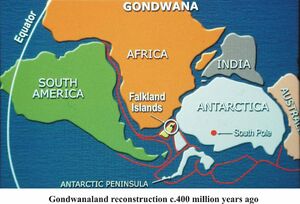 |
| Η αρχαιόηπειρος Gondwana λίγο μετά το σπάσιμό της στα κομμάτια που στην συνέχεια θα απομακρυνθούν και θα μετεξελιχθούν στις σύγχρονες Ηπείρους |
Αν λοιπόν ήταν λογικό και εποικοδομητικό
να αναρωτηθούμε για το σχήμα των αντικειμένων της Γεωλογίας
γιατί να είναι παράλογο
να αναρωτηθούμε για το σχήμα των αντικειμένων της Γεωμετρίας???
Ας σημειωθεί ότι οι δύο αυτές Καμπύλες (Έλλειψη και Υπερβολή)
είναι τόσο θεμελιώδεις στην Γεωμετρία
όσο και οι Ήπειροι στην Γεωγραφία
(Όλες οι καμπύλες της Γεωμετρίας παράγονται από αυτές τις δύο
καθώς και μερικές άλλες που θα αναφέρουμε αργότερα
Θα μπορούσαμε να τις αντιστοιχήσουμε με τους 10 αριθμούς
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9)
του Δεκαδικού Συστήματος της Αριθμητικής
από τους οποίους παράγονται όλοι οι άπειροι υπόλοιποι αριθμοί)
Ας το ψάξουμε λοιπόν.
-----
Ας ξαναδούμε το σχήματα της Έλλειψης και της Υπερβολής.
- Το πρώτο, της Έλλειψης
είναι ενιαίο, ευλογοφανές, αρμονικό, τέλειο.


- Το δεύτερο, της Υπερβολής
είναι κομμένο σε δύο κλαδους, αδιανόητο, αναρμονικό, ατελές
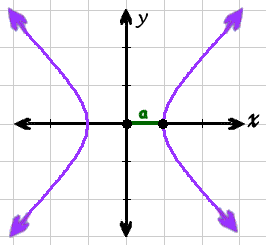

πως είναι δυνατόν
αυτές οι δύο Θεμελιώδεις Καμπύλες
να έχουν τόσο διαφορετικά σχήματα
ενώ οι εξισώσεις τους είναι σχεδόν ίδιες
και διαφέρουν μόνον σε ένα πρόσημο "μείον"????
Η Κλασσική Γεωμετρία απαντά, μέχρι σήμερα, επιγραμματικά:
- Έτσι τις σχημάτισε η Φύση (ή εναλλακτικά, ο Θεός)
Εδώ, λοιπόν, επεμβαίνει η Πολυδιαστατική Θεωρία!
Πριν προχωρήσουμε ας ξαναδούμε το πρώτο χάρτη
στην αρχή της σελίδας, προσεκτικότερα.
 |
| Ειρηνικός Ωκεανός (Pacific Ocean) και στα δεξιά (ανατολικά) και αριστερά (δυτικά) του χάρτη |
Ότι αν ξεκινήσουμε από ένα κέντρο
(π.χ. ένα σημείο του Ισημερινού, έστω στην Αφρική)
που μπορούμε να το αποκαλέσουμε μηδέν (0)
τότε
είτε πηγαίνοντας ανατολικά (+), είτε πηγαίνοντας δυτικά (-),
συναντάμε τον Ειρηνικό Ωκεανό!
Ένας άνθρωπος της Αρχαιότητας θα πάθαινε σοκ από την έκπληξη.
Εμείς, όμως, στην Σύγχρονη Εποχή,
γνωρίζουμε ότι η Γη δεν είναι επίπεδη
και δεν έχει μόνον "εμπρόσθια" πλευρά
(που είμαστε εμείς και το "μηδέν")
αλλά είναι σφαιρική
οπότε έχει και "οπίσθια" πλευρά
(που καλύπτεται από τον Ειρηνικό Ωκεανό κ
αι έχει και ένα άλλο "μηδέν")!
Θαυμάσια, έως εδώ!
--------------
Πάμε, τώρα, να ξαναδούμε την Υπερβολή.
Οι δύο κλάδοι της Υπερβολής
μπορούν να αντιστοιχηθούν κάλλιστα
με τις δύο ακτές του Ειρηνικού, στον πρώτο χάρτη!
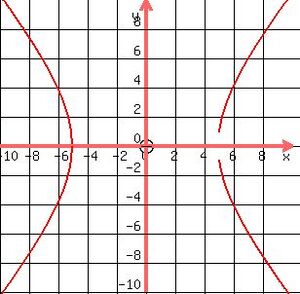 |
| Ο άξονας (x) αντιστοιχίζεται με τον Ισημερινό Ο άξονας (y) αντιστοιχίζεται με τον Πρώτο Μεσημβρινό και οι δύο κλάδοι της Υπερβολής με τις 2 ακτές του Ειρηνικού |
Για να έχουμε μια πιο ολοκληρωμένη εικόνα
ας δούμε Έλλειψη και Υπερβολή μαζί
Η αντιστοίχιση με τον πρώτο χάρτη είναι τώρα εμφανής
- Η Έλλειψη αντιστοιχεί στο συγκρότημα των Ηπείρων
της δικής μας, της "εμπρόσθιας", της "θεατής" πλευράς του Χώρου
(δηλ. στον Χώρο Υπαρκτής Πραγματικότητας
με τις Πραγματικές "ερυθρές" Διαστάσεις)
- Οι δύο κλάδοι της Υπερβολής αντιστοιχούν στις δύο ακτές του Ειρηνικού
που βρίσκεται, ενιαίος, στην "οπίσθια" πλευρά, την "αθέατη πλευρά" του Χώρου
(δηλ. στον Χώρο Εικονικής Πραγματικότητας
με τις Φανταστικές ("καστανόχροες") Διαστάσεις
 |
| Η "πράσινη" Έλλειψη ανάμεσα στους δύο "ερυθρούς" κλάδους της Υπερβολής Η αντιστοίχηση με τον πρώτο χάρτη είναι προφανής. |
Που μας οδηγεί μια τέτοια θέαση?
Ότι αν προχωρήσουμε σε άπειρη απόσταση
θα φτάσουμε στην "οπίσθια" δηλ. στην "αθέατη" πλευρά του Χώρου
(δηλαδή στον Χώρο της Εικονικής Πραγματικότητας)
και τελικά θα φτάσουμε στο "άλλο σημείο 0"
(δηλ. στο σημείο "άπειρο" () που βρίσκεται στο κέντρο της).
Άρα?
Άρα, στον δικό μας "εμπρόσθιο" 3-διάστατο Πραγματικό Χώρο
η Έλλειψη είναι ενιαία αλλά η Υπερβολή είναι δι-κλαδική
ενώ στον "οπίσθιο" 3-διάστατο Φανταστικό Χώρο
συμβαίνει το αντίθετο
η Έλλειψη είναι δι-κλαδική και η Υπερβολή ενιαία!
Επομένως,
στον Μικτό Χώρο (με μία Πραγματική και μία Φανταστική Διάσταση)
η Υπερβολή καλώς έχει πρόσημο (+) καθόσον εκεί είναι ενιαία.

Αντίθετα,
σε έναν τέτοιο 2-δισδιάστατο Μικτό Χώρο
(δηλ. Χώρο Επηυξημένης Πραγματικότητας),
η Έλλειψη θα έχει δύο κλάδους.
Το τελικό συμπέρασμα είναι ότι μπορούμε να καταστήσουμε
το σχήμα της Υπερβολής, ενιαίο,
απλά, αλλάζοντας τον έναν Πραγματικό άξονά της, με τον αντίστοιχο Φανταστικό.
(πράξη που ισοδυναμεί στο παράδειγμά μας
με το να στέψουμε την Γη από την άλλη πλευρά.)
Αυτή η παρατήρηση έχει κολοσσιαία σημασία
όταν στο μεθεπόμενο μέρος
δούμε τις "ιατρικές" (!) επιπτώσεις της Πολυδιαστατικής παρουσίασης
της Υπερβολής.
--------------------------------
ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:
 |
Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου: το ροδόχροο (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου το ροδόχροο (t) = η Διάσταση του Πραγματικού Χρόνου το μαύρο (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου
το κυανό (t) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος) τα γλαυκά (z, y, x) οι Διαστάσεις του Φανταστικού Χώρου (ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος) το κκυανό (q) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου |
-------------------------------------------------------------------
--------------------------------------------------------------------
 ) που βρίσκεται στο κέντρο της).
) που βρίσκεται στο κέντρο της).
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου