Ηλεκτρομαγνητισμός αλά Mendeleev
-A-10-
--------------------------------------------------------------------
--------------------------------------------------------------------
Υπενθυμίζουμε ότι αυτό που παρακολουθούμε
σε αυτήν την σειρά αναρτήσεων
είναι η εποποιία της Εξέλιξης στην, απώτατα, πρώιμη εποχή
- πριν την δημιουργία Ύλης και Ενέργειας
- πριν την δημιουργία του Σύμπαντός μας
- πριν την δημιουργία του Πολυσύμπαντος
Σε μια τόσο μακρινή εποχή
(που η Φυσική και οι Επιστήμες δεν είχαν λόγο ύπαρξης)
αυτές που "αλώνιζαν ασύδοτες"
ήταν οι Διαστάσεις που συνδυαζόμενες μεταξύ τους
δημιουργούσαν τα Θεμελιώδη Σχήματα
από τα οποία, αργότερα με "μετάλλαξη", θα προέκυπταν
τα Πεδία, η Ενέργεια και η Ύλη
Υπενθυμίζουμε ότι αυτό που παρακολουθούμε
σε αυτήν την σειρά αναρτήσεων
είναι η εποποιία της Εξέλιξης στην, απώτατα, πρώιμη εποχή
- πριν την δημιουργία Ύλης και Ενέργειας
- πριν την δημιουργία του Σύμπαντός μας
- πριν την δημιουργία του Πολυσύμπαντος
Σε μια τόσο μακρινή εποχή
(που η Φυσική και οι Επιστήμες δεν είχαν λόγο ύπαρξης)
αυτές που "αλώνιζαν ασύδοτες"
ήταν οι Διαστάσεις που συνδυαζόμενες μεταξύ τους
δημιουργούσαν τα Θεμελιώδη Σχήματα
από τα οποία, αργότερα με "μετάλλαξη", θα προέκυπταν
τα Πεδία, η Ενέργεια και η Ύλη
Στο σημερινό μέρος θα δούμε
άλλη μία δημιουργία ενός Θεμελιώδους Σχήματος
που δημιουργείται, ακραιφνώς, από την Εξέλιξη,
με μόνη συνέργεια, αυτήν της Συμμετρίας.
Στα προηγούμενα είχαμε γνωρίσει τα εξής:
1) το Ελλειψοειδές, 2) το Υπερβολοειδές και
3) τον Ελλειπτικό Κύλινδρο
Τι λείπει λοιπόν?
Δεν χρειάζεται νάχει κάποιος ιδιαίτερη νοημοσύνη
ή βαθειές γνώσεις για να το αντιληφθεί.
Η Συμμετρία (και η νοητική "μέθοδος των τριών") δίνουν την απάντηση:
4) ο Υπερβολικός Κύλινδρος!
Ας υπενθυμίσουμε, λοιπόν, και πάλι, τα 3 προρρηθέντα Σχήματα
και τις εξισώσεις που τα περιγράφουν.
άλλη μία δημιουργία ενός Θεμελιώδους Σχήματος
που δημιουργείται, ακραιφνώς, από την Εξέλιξη,
με μόνη συνέργεια, αυτήν της Συμμετρίας.
Στα προηγούμενα είχαμε γνωρίσει τα εξής:
1) το Ελλειψοειδές, 2) το Υπερβολοειδές και
3) τον Ελλειπτικό Κύλινδρο
Τι λείπει λοιπόν?
Δεν χρειάζεται νάχει κάποιος ιδιαίτερη νοημοσύνη
ή βαθειές γνώσεις για να το αντιληφθεί.
Η Συμμετρία (και η νοητική "μέθοδος των τριών") δίνουν την απάντηση:
4) ο Υπερβολικός Κύλινδρος!
Ας υπενθυμίσουμε, λοιπόν, και πάλι, τα 3 προρρηθέντα Σχήματα
και τις εξισώσεις που τα περιγράφουν.
Η αλγεβρική εξίσωση που περιγράφει το Ελλειψοειδές,
στην Κλασσική Γεωμετρία, είναι:
 |
| Προσθήκη λεζάντας |
2) Το Μονόχωνο Υπερβολοειδές (Μέρος Α - 04):

Η αλγεβρική εξίσωση που περιγράφει το Μονόχωνο Υπερβολοειδές,
στην Κλασσική Γεωμετρία, είναι:

3) ο Ελλειπτικός Κύλινδρος (Μέρος A - 09)
Η αλγεβρική εξίσωση που περιγράφει τον Ελλειπτικό Κύλινδρο
στην Κλασσική Γεωμετρία, είναι:
4) Πάμε τώρα να παρουσιάσουμε τον Υπερβολικό Κύλινδρο (Μέρος Α - 10)
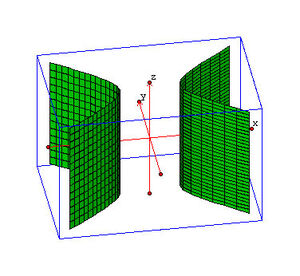
στην Κλασσική Γεωμετρία, είναι:
 |
| Προσθήκη λεζάντας |
------------
Όπως, έχουμε προαναφέρει, η Πολυδιαστατική Θεωρία
παρέχει μία ενιαία μορφή των εξισώσεων αυτών.
Έχουμε λοιπόν:
- Η αλγεβρική εξίσωση που περιγράφει το Ελλειψοειδές,
στην Πολυδιαστατική Γεωμετρία,
είναι:
- Η αλγεβρική εξίσωση που περιγράφει το Μονόχωνο Υπερβολοειδές,
στην Πολυδιαστατική Γεωμετρία,
είναι:
- Η αλγεβρική εξίσωση που περιγράφει τον Ελλειπτικό Κύλινδρο
στην Πολυδιαστατική Γεωμετρία,
είναι:
- Οπότε, αντίστοιχα, αλγεβρική εξίσωση που περιγράφει τον Υπερβολικό Κύλινδρο
στην Πολυδιαστατική Γεωμετρία,
θα είναι:
-----------------------
Υπενθυμίζουμε ότι:
- Οι μεν "ερυθροί" άξονες (x , y, z)
των Διαστάσεων του Πραγματικού τρισ-διδιάστατου 3D-Χώρου
έλκουν τα άκρα και απωθούν το μέσο της ελαστικής καμπύλης, αλλιώς "χορδής",
αναγκάζοντάς την να τους τμήσει σε 2 σημεία τους.
- Οι δε "γαλάζιοι" άξονες (x , y, z)
των Διαστάσεων του Φανταστικού τρισ-διδιάστατου 3D-Χώρου
έλκουν το μέσον και απωθούν τα άκρα της ελαστικής καμπύλης, αλλιώς "χορδής",
αναγκάζοντάς την να μην τους τμήσει σε κάποιο σημείο τους.
- Ο δε "ροδόχροος" άξονας (t)
της Διάστασης του Πραγματικού Χρόνου
δεν έλκει ούτε απωθεί αλλά απαγορεύει στην "χορδή" να τον τμήσει
σε κάποιο σημείο του
(ή ισοδύναμα, η τομή γίνεται στο άπειρο)
παρέχει μία ενιαία μορφή των εξισώσεων αυτών.
Έχουμε λοιπόν:
- Η αλγεβρική εξίσωση που περιγράφει το Ελλειψοειδές,
στην Πολυδιαστατική Γεωμετρία,
είναι:
 |
| Προσθήκη λεζάντας |
- Η αλγεβρική εξίσωση που περιγράφει το Μονόχωνο Υπερβολοειδές,
στην Πολυδιαστατική Γεωμετρία,
είναι:
 |
| Προσθήκη λεζάντας |
- Η αλγεβρική εξίσωση που περιγράφει τον Ελλειπτικό Κύλινδρο
στην Πολυδιαστατική Γεωμετρία,
είναι:
 |
| Προσθήκη λεζάντας |
- Οπότε, αντίστοιχα, αλγεβρική εξίσωση που περιγράφει τον Υπερβολικό Κύλινδρο
στην Πολυδιαστατική Γεωμετρία,
θα είναι:
 |
| Προσθήκη λεζάντας |
-----------------------
Υπενθυμίζουμε ότι:
- Οι μεν "ερυθροί" άξονες (x , y, z)
των Διαστάσεων του Πραγματικού τρισ-διδιάστατου 3D-Χώρου
έλκουν τα άκρα και απωθούν το μέσο της ελαστικής καμπύλης, αλλιώς "χορδής",
αναγκάζοντάς την να τους τμήσει σε 2 σημεία τους.
- Οι δε "γαλάζιοι" άξονες (x , y, z)
των Διαστάσεων του Φανταστικού τρισ-διδιάστατου 3D-Χώρου
έλκουν το μέσον και απωθούν τα άκρα της ελαστικής καμπύλης, αλλιώς "χορδής",
αναγκάζοντάς την να μην τους τμήσει σε κάποιο σημείο τους.
- Ο δε "ροδόχροος" άξονας (t)
της Διάστασης του Πραγματικού Χρόνου
δεν έλκει ούτε απωθεί αλλά απαγορεύει στην "χορδή" να τον τμήσει
σε κάποιο σημείο του
(ή ισοδύναμα, η τομή γίνεται στο άπειρο)
--------------------------------
ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:
-------------------------------------------------------------------
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:
 |
Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου: το ροδόχροο (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου το ροδόχροο (t) = η Διάσταση του Πραγματικού Χρόνου το μαύρο (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου
το κυανό (t) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος) τα γλαυκά (z, y, x) οι Διαστάσεις του Φανταστικού Χώρου (ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος) το κκυανό (q) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου |
--------------------------------------------------------------------



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου