Ηλεκτρομαγνητισμός αλά Mendeleev
-C-05-
--------------------------------------------------------------------
--------------------------------------------------------------------
Στο προηγούμενο είχαμε επισημάνει ότι
η επαναφορά της Οικουμενικής Συμμετρίας
στους Φυσικούς Νόμους του Ηλεκτρομαγνητισμού
είναι κομβική επειδή
εξασφαλίζει την διατήρηση της Συναλλοιότητας των εξισώσεων
που, απλοϊκά, ισοδυναμεί με την διατύπωση τους
στην "Γεωμετρική Γλώσσα"
ή αλλιώς "Τανυστική γλώσσα"
ή (για τους μυημένους) "Γλώσσα της Διαφορικής Γεωμετρίας"
ώστε όλοι οι Παρατηρητές απανταχού του Σύμπαντος
να παίρνουν τα σωστά αποτελέσματα.
Πριν προχωρήσουμε στην "ανακαίνιση" του Φυσικού Χώρου
απορρίπτοντας τον 3-διάστατο Ευκλείδειο Χώρο
και υιοθετώντας τον 4-διάστατο Χώρο Minkowski
θα δώσουμε ένα απλούστατο παράδειγμα
που θα καταδείξει
γιατί η χρήση της "Γεωμετρικής ή Τανυστικής Γλώσσας"
είναι ο μοναδικός φωτεινός οδηγός μας.
Ας μεταφερθούμε λοιπόν στις απαρχές της Φυσικής Επιστήμης
και ας παρακολουθήσουμε έναν μονο-διάστατο "Άνθρωπο"-φυσικό
που προσπαθεί να περιγράψει το Φυσικό Φαινόμενο της Κίνησης
στον Μονο-διάστατο Χώρο του.
Οι μονο-διάστατοι φυσικοί, δύσκολα ή εύκολα, κατέληξαν
στον Νόμο της Ομαλής Κίνησης που συνδέει τα 3 φυσικά μεγέθη της.
Στο προηγούμενο είχαμε επισημάνει ότι
η επαναφορά της Οικουμενικής Συμμετρίας
στους Φυσικούς Νόμους του Ηλεκτρομαγνητισμού
είναι κομβική επειδή
εξασφαλίζει την διατήρηση της Συναλλοιότητας των εξισώσεων
που, απλοϊκά, ισοδυναμεί με την διατύπωση τους
στην "Γεωμετρική Γλώσσα"
ή αλλιώς "Τανυστική γλώσσα"
ή (για τους μυημένους) "Γλώσσα της Διαφορικής Γεωμετρίας"
ώστε όλοι οι Παρατηρητές απανταχού του Σύμπαντος
να παίρνουν τα σωστά αποτελέσματα.
Πριν προχωρήσουμε στην "ανακαίνιση" του Φυσικού Χώρου
απορρίπτοντας τον 3-διάστατο Ευκλείδειο Χώρο
και υιοθετώντας τον 4-διάστατο Χώρο Minkowski
θα δώσουμε ένα απλούστατο παράδειγμα
που θα καταδείξει
γιατί η χρήση της "Γεωμετρικής ή Τανυστικής Γλώσσας"
είναι ο μοναδικός φωτεινός οδηγός μας.
Ας μεταφερθούμε λοιπόν στις απαρχές της Φυσικής Επιστήμης
και ας παρακολουθήσουμε έναν μονο-διάστατο "Άνθρωπο"-φυσικό
που προσπαθεί να περιγράψει το Φυσικό Φαινόμενο της Κίνησης
στον Μονο-διάστατο Χώρο του.
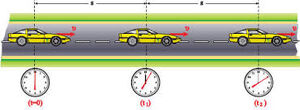 |
| Ευθύγραμμη Ομαλή Κίνηση --- Για την περιγραφή της αρκούν τρία φυσικά μεγέθη 1) η απόσταση (s) μεταξύ αρχικής και τελικής θέσης 2) ο χρόνος (t) της διάρκειας της κίνησης 3) η ταχύτητα (v) του κινούμενου σώματος |
 |
| Οριζόντια Ευθύγραμμη Ομαλή κίνηση |
Οι μονο-διάστατοι φυσικοί, δύσκολα ή εύκολα, κατέληξαν
στον Νόμο της Ομαλής Κίνησης που συνδέει τα 3 φυσικά μεγέθη της.
 |
δηλαδή, η απόσταση (s)
ισούται με το γινόμενο της ταχύτητας (vs ) της οριζόντιας κίνησης του σώματος
επί τον χρόνο (t) της κίνησης
|
 |
| Κατακόρυφη Ευθύγραμμη Ομαλή Κίνηση |
 |
δηλαδή, η ανύψωση (h)
ισούται με το γινόμενο της ταχύτητας (vh ) της κατακόρυφης κίνησης του σώματος
επί τον χρόνο (t) της κίνησης
|
Πρέπει να ξεκαθαριστεί ότι οι μονοδιάστατοι φυσικοί
θεωρούν αυτά τα δύο φυσικά μεγέθη
(δηλ. την απόσταση (s) και την ανύψωση (h) )
τελείως διαφορετικά μεταξύ τους, χωρίς κάποιον συσχετισμό.
---------------------------------------------------------------------------------------------------
Για όσους απορούν για το πως γίνεται
ο μονο-διάστατος Παρατηρητής να παρατηρεί,
εκτός από αποστάσεις, και ανυψώσεις σε "άλλο άξονα"
εκτός από αποστάσεις, και ανυψώσεις σε "άλλο άξονα"
θα ξεκαθαρίσουμε ότι δεν πρόκειται για "άλλο άξονα"
αλλά για την ίδια Διάσταση που απλά περιστρέφεται
(χωρίς, βέβαια, αυτό να το γνωρίζουν οι "κάτοικοί" της)
οπότε, οι "ιθαγενείς" μονοδιάστατοι φυσικοί
- την μία φορά (την "ημέρα") μετρούν το φυσικό μέγεθος, Απόσταση (s)
- και την άλλη φορά (την "νύκτα") μετρούν το φυσικό μέγεθος, Ανύψωση (h)
------------------------------------------------------------------------------------------------------
Αν παρατηρήσει κάποιος, προσεκτικά, τους δύο αυτούς νόμους
θα αντιληφθεί ότι είναι εντελώς αντίστοιχοι
με τους νόμους του Πίνακα, αντίστοιχα
για το Μαγνητικό Πεδίο και το Ηλεκτρικό Πεδίο
Πράγματι, οι νόμοι αυτοί συνδέουν δύο φυσικά μεγέθη άμεσα μεταξύ τους
με την μεσολάβηση ενός τελεστή που,
στην παρούσα περίπτωση,
αντιπροσωπεύει ο χρόνος (t).
Οι μονοδιάστατοι φυσικοί, λοιπόν, διατύπωσαν
Φυσικούς Νόμους που είχαν Οικουμενική Συμμετρία (global symmetry)
και έδιναν τα ίδια ακριβώς αποτελέσματα
σε όλους τους Παρατηρητές,
σε οποιοδήποτε σημείο του Μονοδιάστατου Σύμπαντος,
κι αν βρίσκονταν.
Όλα ήταν ειδυλλιακά, λοιπόν, στο Μονοδιάστατο Σύμπαν
μέχρι που ... στον δισ-Διάστατο Χώρο
συνέβη ένα (δισ-διάστατο φαινόμενο) (!)
Δηλαδή, εκτοξεύθηκε ένα "επίπεδο" βλήμα
και η τροχιά του καμπυλώθηκε
εξ αιτίας των προαναφερθέντων "Επαγωγικών Φαινομένων"
(αντίστοιχα με αυτά που γνωρίσαμε στο Μέρος C-02 )
που στην παρούσα περίπτωση
μπορεί να είναι η Βαρύτητα
(ή εναλλακτικά,
- ένας άνεμος που στρεβλώνει την ευύγραμμη πτήση ενός πτηνού
- ή ένα θαλάσσιο ρεύμα που στρεβλώνει την ευθύγραμμη πλεύση ενός πλοίου)
θα αντιληφθεί ότι είναι εντελώς αντίστοιχοι
με τους νόμους του Πίνακα, αντίστοιχα
για το Μαγνητικό Πεδίο και το Ηλεκτρικό Πεδίο
Πράγματι, οι νόμοι αυτοί συνδέουν δύο φυσικά μεγέθη άμεσα μεταξύ τους
με την μεσολάβηση ενός τελεστή που,
στην παρούσα περίπτωση,
αντιπροσωπεύει ο χρόνος (t).
Οι μονοδιάστατοι φυσικοί, λοιπόν, διατύπωσαν
Φυσικούς Νόμους που είχαν Οικουμενική Συμμετρία (global symmetry)
και έδιναν τα ίδια ακριβώς αποτελέσματα
σε όλους τους Παρατηρητές,
σε οποιοδήποτε σημείο του Μονοδιάστατου Σύμπαντος,
κι αν βρίσκονταν.
Όλα ήταν ειδυλλιακά, λοιπόν, στο Μονοδιάστατο Σύμπαν
μέχρι που ... στον δισ-Διάστατο Χώρο
συνέβη ένα (δισ-διάστατο φαινόμενο) (!)
Δηλαδή, εκτοξεύθηκε ένα "επίπεδο" βλήμα
και η τροχιά του καμπυλώθηκε
εξ αιτίας των προαναφερθέντων "Επαγωγικών Φαινομένων"
(αντίστοιχα με αυτά που γνωρίσαμε στο Μέρος C-02 )
που στην παρούσα περίπτωση
μπορεί να είναι η Βαρύτητα
(ή εναλλακτικά,
- ένας άνεμος που στρεβλώνει την ευύγραμμη πτήση ενός πτηνού
- ή ένα θαλάσσιο ρεύμα που στρεβλώνει την ευθύγραμμη πλεύση ενός πλοίου)
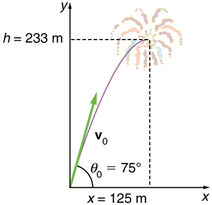 |
| όπου h = ανύψωση και x = απόσταση (s) |
Οι μονοδιάστατοι φυσικοί, έκαναν, όπως πάντα, τις μετρήσεις τους
και αρχικά, καθώς τα όργανά τους δεν είχαν ακόμη εξελιχθεί
δεν σημείωσαν κάτι περίεργο
Όταν, όμως, τα όργανά τους τελειοποιήθηκαν
και οι μετρήσεις τους έγιναν ακριβείς
τότε παρατήρησαν, καθαρά πλέον, μία απόκλιση
της τιμής της ανύψωσης (h) που έδινε ο Φυσικός Νόμος τους
από την τιμή που έδειχνε η μετρητική συσκευή τους.
Η απόκλιση αυτή οφειλόταν σε έναν επιπλέον όρο στην εξίσωση
εξ αιτίας της ύπαρξης της βαρύτητας
 |
| Προσθήκη λεζάντας |
Αυτό, όπως ήταν φυσικό, προκάλεσε θύελλα αντιδράσεων
στο Μονοδιάστατο Σύμπαν

Αμέσως κυκλοφόρησαν και βιβλία για να διακυρήξουν
ότι οι Φυσικοί Νόμοι ψεύδονται
ότι οι Φυσικοί Νόμοι ψεύδονται

Και, όπως ήταν επόμενο, παρενέβη και η Θρησκεία
για να δηλώσει ότι το "χέρι του Θεού"
είναι αυτό που παρεμβαίνει και ακυρώνει τους Φυσικούς Νόμους
για να σημειωθεί θαύμα
και έτσι οι μονοδιάστατοι άνθρωποι
να επιστρέψουν και πάλι στον δρόμο του Θεού.
για να δηλώσει ότι το "χέρι του Θεού"
είναι αυτό που παρεμβαίνει και ακυρώνει τους Φυσικούς Νόμους
για να σημειωθεί θαύμα
και έτσι οι μονοδιάστατοι άνθρωποι
να επιστρέψουν και πάλι στον δρόμο του Θεού.

Οι φυσικοί του Μονοδιάστατου Σύμπαντος έπεσαν σε απελπισία.
Πως γίνεται να δίνουν λάθος αποτελέσματα οι εξισώσεις τους?
Να είναι, πραγματικά, ο Ύψιστος ο υπαίτιος?
 |
| Πως είναι δυνατόν να δίνουν λάθος αποτελέσματα οι εξισώσεις, γαμώτο??? |
-------------------------------------------------------------------
--------------------------------------------------------------------



Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου