Electromagnetism a la Mendeleev - C-04

Ηλεκτρομαγνητισμός αλά Mendeleev
-C-04-

C. Ηλεκτροδυναμική
Οικουμενική Συμμετρία

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στα Μαθηματικά και στην Φυσική
υπάρχουν κάποιες έννοιες που,
παραφορτωμένες με πολύπλοκους μαθηματικούς συμβολισμούς,
φαντάζουν απίστευτα περίπλοκες
ενώ
ουσιαστικά είναι αυτονόητες.

Θα ασχοληθούμε με δύο από αυτές:
- την αναλλοιότητα (invariance) και
- την συναλλοιότητα (covariance)

Για να τις κατανοήσουμε πρέπει να τις αντιστοιχίσουμε
με έννοιες της Καθημενότητας

Ας πάμε στην Γλωσσολογία
Ενδιαφερόμαστε για αναλλοίωτα "λεξικά αντικείμενα" που υπάρχουν
στις Γλώσσες της Γης

Αυτά είναι, προφανώς, κάποια επιφωνήματα
όπως π.χ. το επιφώνημα αιφνιδιασμού, έκπληξης πόνου κλπ

Το επιφώνημα "Ωχ"
είναι αναλλοίωτο
σε όλες, σχεδόν, τις Γλώσσες της Γης
Όποιος άνθρωπος
αιφνιδιαστεί, πονέσει, εκπλαγεί
αυτό το επιφώνημα θα αναφωνήσει
ανεξάρτητα από την Γλώσσα ομιλίας του.

Αντίστοιχα, λοιπόν, υπάρχουν και στην Φυσική
κάποια Φυσικά Μεγέθη που παραμένουν αναλλοίωτα
σε όποια περιοχή του Σύμπαντος και να βρεθεί κάποιος (ως Παρατηρητής)
π.χ. η μάζα (m) ενός αντικειμένου

H Μάζα (m)
ενός αντικειμένου
που είναι στην Γη
π.χ. 1 kilogram
θα έχει αναλλοίωτη τιμή
είτε μετρηθεί στον Άρη, είτε στην Σελήνη
είτε οπουδήποτε στο Σύμπαν
όμως
για ένα άλλο φυσικό μέγεθος
δηλ. το Βάρος (W)
δεν θα συμβεί.
Αυτό θα αλλάξει τιμή
ανάλογα με τον Πλανήτη
πάνω στον οποίο βρίσκεται το αντικείμενο

Όμως, οι υπόλοιπες λέξεις δεν είναι αναλλοίωτες.

Οι περισσότερες λέξεις
δεν είναι, προφανώς, αναλλοίωτες
π.χ. η λέξη "καλημέρα"
αποδίδεται πολύ διαφορετικά
σε άλλες Γλώσσες.

Δεν αρκεί η επικοινωνία
μεταξύ πομπού και δέκτη
Απαιτείται και διερμηνεία.
Π.χ.
την Ηχητική Μεταφορά
της λέξης "δεν",
ένας Άγγλος,
θα την εκλάβει ως "then" (= τότε)
Η συναλλοιότητα λοιπόν
είναι ταυτόσημη έννοια με την διερμηνεία

Από τα προαναφερθέντα προκύπτει
ότι Φυσικά Μεγέθη και Φυσικοί Νόμοι πρέπει να διατηρούν
τόσο την αναλλοιότητα όσο και την συναλλοιότητα των δεδομένων της Φύσης

Ε ... ακριβώς αυτό διασφαλίζει ο Τανυστικός Λογισμός

Ουσιαστικά, αυτός είναι μία Πανσυμπαντική γλώσσα που πιστοποιεί
ότι ο κάθε Παρατηρητής,
ανεξάρτητα σε ποιά περιοχή του Σύμπαντος βρίσκεται,
και ανεξάρτητα από την εποχή που ζει,
θα "διαβάσει σωστά" την κάθε εξίσωση της Φυσικής
(εφόσον αυτές είναι γραμμένες "τανυστικά")
και θα πάρει τα ορθά αποτελέσματα.

Επανερχόμαστε, λοιπόν, στον Ηλεκτρομαγνητισμό
Οι πίνακες με τις εξισώσεις του Μέρους B-12b
(χωρίς την ύπαρξη επαγωγικών φαινομένων)
μπορούν να γραφούν σε τανυστική μορφή
αντίθετα
οι πίνακες με τις εξισώσεις του Μέρους C-02a
(που συμπεριλαμβάνουν τα Επαγωγικά Φαινόμενα)
δεν γίνεται να γραφούν (όλες) σε τανυστική μορφή.

ΣΗΜ: Υπενθυμίζουμε ότι Επαγωγικά Φαινόμενα είναι:
- το Φαινόμενο της Ηλεκτρικής Μετατόπισης
- το Φαινόμενο της Μαγνητικής Επαγωγής

Για να εμπεδώσουμε περισσότερο την "καταστροφή" που
προκαλεί η ύπαρξη των Επαγωγικών Φαινομένων
ας φανταστούμε την ύπαρξη, μέσα στον Χώρο,
νοητών "δυναμικών" γραμμών
- Οι "κάθετες" γραμμές  δείχνουν την διεύθυνση που "φυσάει"
το Ηλεκτρικό Πεδίο (ή εναλλακτικά, το Ηλεκτρικό Φορτίο)
 - Οι "οριζόντιες" γραμμές  δείχνουν την διεύθυνση που "φυσάει"
το Μαγνητικό Πεδίο (ή εναλλακτικά, το Ηλεκτρικό Ρεύμα)

Στην περίπτωση
που δεν υπάρχουν Επαγωγικά Φαινόμενα
οπότε δεν υπάρχει Χρόνος,
(δηλ. υπάρχει μόνον "τετελεσμένο" Παρόν)
τότε
οι Φυσικές Οντότητες δεν σχετίζονται μεταξύ τους,
κάθε σωματίδιο ή υλικό σώμα της Φύσης
δέχεται επίδραση
μόνον από την Οντότητα που το επηρεάζει
οπότε κινείται ανάλογα
κατά μήκος των δυναμικών γραμμών
(ή κάθετα, ή οριζόντια)
Οπότε,
ο Χώρος εμφανίζεται "αστρέβλωτος"
(όπως, είναι το λογικό),
δηλ. επικρατεί αρμονία
και η Φυσική αποκαλεί
την συμμετρία της αρμονίας αυτής,
Οικουμενική Βαθμιδική Συμμετρία
(global gauge symmetry)

Στην περίπτωση
που υπάρχουν Επαγωγικά Φαινόμενα
οπότε υπάρχει Χρόνος
(δηλ. υπάρχουν Παρελθόν, Παρόν και Μέλλον)
τότε
οι Φυσικές Οντότητες σχετίζονται μεταξύ τους
και
κάθε σωματίδιο ή υλικό σώμα της Φύσης
δέχεται επίδραση
και από άλλη Οντότητα εκτός από την "δική του"
οπότε κινείται μεν
κατά μήκος των (στρεβλών πλέον) δυναμικών γραμμών
(δηλ. "λοξά")
Οπότε
ο Χώρος εμφανίζεται "στρεβλωμένος"
(κάτι που δεν είναι λογικό),
δηλ. επικρατεί δυσαρμονία
και η Φυσική αποκαλεί
την συμμετρία της δυσαρμονίας αυτής
"Τοπική Βαθμιδική Συμμετρία"
(local gauge symmetry)

Μία, ίσως, καλύτερη εμπέδωση της διαφοράς μεταξύ
της Οικουμενικής (global) και της Τοπικής (local) συμμετρίας
δίνεται από το επόμενο σχήμα
Ας θεωρήσουμε, περισσότερο ρεαλιστικά,
ένα υλικό σώμα στην επιφάνεια της Γης
Οι νοητές γραμμές (κατ' αντιστοιχία, μεσημβρινοί και παράλληλοι)
έχουν την ίδια σημασία όπως και στο προηγούμενο παράδειγμα.
Στην πρώτη "νηνεμιακή" σφαίρα
δεν υπάρχουν Φυσικές Οντότητες που να "φυσούν".
- στην δεύτερη σφαίρα οι Φυσικές Οντότητες υπάρχουν
  αλλά δεν σχετίζονται μεταξύ τους
  (καθώς δεν υπάρχουν επαγωγικά φαινόμενα)
  και επικρατεί η Οικουμενική (global) συμμετρία
  οπότε αυτή δεν εμφανίζει διαφορές από την πρώτη σφαίρα
- στην τρίτη σφαίρα οι Φυσικές Οντότητες υπάρχουν
   αλλά σχετίζονται μεταξύ τους
   (καθώς δεν υπάρχουν επαγωγικά φαινόμενα)

   οπότε επικρατεί η Τοπική (local) συμμετρία
   (το σκηνικό είναι εντελώς ανάλογο ως να "φυσούν" αληγείς άνεμοι
    ή ισοδύναμα να επιδρούν δυνάμεις Coriolis)
   οπότε οι διαφορές της από την πρώτη "νηνεμιακή" σφαίρα
   είναι εμφανείς

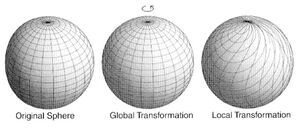Διαφορά
της global και της local συμμετρίας
------
Αν υποθέσουμε ότι ένα Υλικό Σώμα
βρίσκεται στο "Βόρειο Πόλο"
και αφεθεί ελεύθερο
υπό την επίδραση
του Ηλεκτρικού Πεδίου (ή εναλλακτικά του Ηλεκτρικού Φορτίου)
που "φυσά" κατά μήκος ενός μεσηβρινού
που διέρχεται π.χ. από την Αθήνα
τότε
1) αν η συμμετρία του Χώρου είναι
Οικουμενική (global),
το σώμα θα κινηθεί "ίσια"
και θα φθάσει, λογικά, στην Αθήνα
2) αν η συμμετρία του Χώρου είναι
Τοπική (local)
το σώμα θα κινηθεί "λοξά"
και θα φθάσει, παραδόξως, π.χ. στην Ρώμη

Το μειονέκτημα, λοιπόν, των "διορθωμένων" εξισώσεων
του Ηλεκτρομαγνητισμού που αναφέρθηκαν στο Μέρος C-02a
(ώστε να ενσωμάτωσουν τα Επαγωγικά Φαινομένα)
είναι θεμελιώδες και κρίσιμο και όχι τόσο απλό
όσο μπορεί να φαινόταν αρχικά.

Η αδυναμία τους να γραφούν σε "τανυστική γλώσσα"
και έτσι να προσφέρουν στον κάθε Παρατηρητή
μη-αλλοιώσιμα δεδομένα
κλόνιζε όλο το Οικοδόμημα της Φυσικής.
Εκατοντάδες "μεσοβέζικες" λύσεις προτάθηκαν ...
όμως το πρόβλημα δεν αντιμετωπιζόταν
Τι έπρεπε να γίνει???

Ακριβώς αυτό!
Όταν όλες οι προτεινόμενες δυνατές λύσεις
αδυνατούν να λύσουν το πρόβλημα
πρέπει να δράσεις ριζικά και ρηξικέλευθα.
Να αλλάξεις τα "πιστεύω" σου
.... για τον Χώρο

Η λύση δόθηκε, στις αρχές του εικοστού αιώνα (1916),
"συλλογικά" από τον Einstein και αρκετούς ακόμη φυσικούς.
Ήταν η αναβάθμιση του Χώρου (!)
από τρισδιάστατο Ευκλείδειο
(που ήταν συμβατός με τις εμπειρίες του ανθρώπου)
στον τετραδιάστατο Minkoswki
(που ενσωμάτωνε πλήθος από απίστευτες παραδοξότητες όπως,
Διαστολή Χρόνου, Συστολή Μήκους, Παράδοξο των Διδύμων κ.α)

Η απόρριψη
της παραδοχής ότι ζούμε
σε τρισδιάστατο Ευκλείδειο Χώρο
και η παραδοχή
ότι ο Φυσικός Χώρος μας
είναι ο τετραδιάστος Χώρος Minkowski
δεν ήταν καθόλου εύκολη ούτε εύπεπτη.
Ο Άνθρωπος
έπρεπε να αποδεχθεί
ότι οι αισθήσεις και εμπειρίες του
είναι όχι απλά ελλιπείς
αλλά και ελαττωματικές.
Έπρεπε να αποδεχθεί
την ανωτερότητα των εξισώσεων της Φυσικής
σε σχέση, όχι μόνον με την όραση και την αφή του,
αλλά και με την Λογική του.
Ήταν, συνοπτικά,
η καταρράκωση της ανθρώπινης κρίσης
της ανθρώπινης αυτοεκτίμησης,
και της εμπειρικής ορθολογικότητας.

Στα επόμενα θα δούμε πως διαμορφώθηκε το "τοπίο" του Ηλεκτρομαγνητισμού
μετά την "ανακαίνιση" του Φυσικού Χώρου.

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------