Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο10-
Φυσικό μέγεθος.
Εμβαθύνοντας ακόμα περισσότερο
Εμβαθύνοντας ακόμα περισσότερο
--------------------------------------------------------------------
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας
--------------------------------------------------------------------
Η "νοητική μηχανή" είναι ένα καλό παράδειγμα
για να κατανοήσει κάποιος το Φυσικό Μέγεθος
αλλά παραμένει μία ασαφής εικόνα.
Αν θέλουμε να κατανοήσουμε σε μεγαλύτερο βάθος τα πράγματα
πρέπει να μπούμε μέσα στην "νοητική μηχανή"
και να δούμε πως ακριβώς δουλεύει.
Εκεί θα δούμε ότι η "μηχανή" απλά κάνει Μαθηματικές Πράξεις
άρα μπορεί να υποκατασταθεί από μία Αλγεβρική παράσταση
π.χ. f(x) = 10x - 8 +4 ....
Όμως, κάθε Αλγεβρική παράσταση αντιστοιχεί σε μία Γεωμετρική Αναπαράσταση
Επομένως, γενικά, κάθε Φυσικό Μέγεθος ουσιαστικά αντιπροσωπεύεται
από μία συνάρτηση των Διαστάσεων του Χωρόχρονου (x, y, z, t)
και αποδίδεται γεωμετρικά από ένα γεωμετρικό σχήμα.
"μπλέκει" η Άλγεβρα και η Γεωμετρία "μέσα στα πόδια" της Φυσικής.
--------------------------------------------------------------------
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας
--------------------------------------------------------------------
Η "νοητική μηχανή" είναι ένα καλό παράδειγμα
για να κατανοήσει κάποιος το Φυσικό Μέγεθος
αλλά παραμένει μία ασαφής εικόνα.
Αν θέλουμε να κατανοήσουμε σε μεγαλύτερο βάθος τα πράγματα
πρέπει να μπούμε μέσα στην "νοητική μηχανή"
και να δούμε πως ακριβώς δουλεύει.
Εκεί θα δούμε ότι η "μηχανή" απλά κάνει Μαθηματικές Πράξεις
άρα μπορεί να υποκατασταθεί από μία Αλγεβρική παράσταση
π.χ. f(x) = 10x - 8 +4 ....
 |
| Εδώ ένα παράδειγμα "νοητικής μηχανής" που ουσιαστικά αποτελεί οπτική αναπαράσταση της Αριθμητικής παράστασης f(x) = (3 * 5) - 2 |
 |
| Γεωμετρική Παράσταση της αλγεβρικής παράστασης f(x) = 3x+2 |
 |
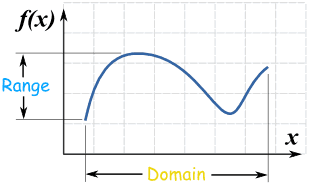
| Άλλες δύο Γεωμετρικές αναπαραστάσεις |
από μία συνάρτηση των Διαστάσεων του Χωρόχρονου (x, y, z, t)
και αποδίδεται γεωμετρικά από ένα γεωμετρικό σχήμα.
"μπλέκει" η Άλγεβρα και η Γεωμετρία "μέσα στα πόδια" της Φυσικής.
--------------------------------------------------------------------
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου