Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο28-
Αναζήτηση
"κρυμμένων" Διαστάσεων
(ι' μέρος)
"κρυμμένων" Διαστάσεων
(ι' μέρος)
--------------------------------------------------------------------
--------------------------------------------------------------------
Υπενθυμίζουμε λοιπόν και πάλι
ότι ένας Χώρος αποτελείται από ένα σύνολο σημείων.
Όμως, ο Χώρος δεν είναι "σκορποχώρι"
Τα σημεία του κάθε Χώρου υπακούουν σε απαρέγκλιτους κανόνες
"ιεραρχίας" και "κοινωνικής συμπεριφοράς"
α) Η "ιεραρχία" εκφράζεται από
τα δύο διανύσματα της μετατόπισης (ή διανύσματα θέσης)
(ανταλλοίωτο και συναλλοίωτο)
που καθορίζουν, επακριβέστατα, την θέση ενός σημείου του Χώρου
β) Η "κοινωνική συμπεριφορά" εκφράζεται από
την μήτρα απειροστής στροφής
που καθορίζει τον "τρόπο σύνδεσης" των σημείων του
με τα γειτονικά τους
Αυτά τα δύο μαθηματικά εργαλεία είναι πλήρως αρκετά
ώστε να παράγουν όλες τις ιδιότητες ενός Χώρου
Και, όπως έχουμε αναφέρει, πολλάκις, στα προηγούμενα
η πλήρης κατανόηση του Χώρου οδηγεί
στην πλήρη κατανόηση της Γεωμετρίας του
(δηλ. των ιδιοτήτων των Γεωμετρικών Σχημάτων
που "φύονται" μέσα σε αυτόν)
ενώ στην συνέχεια
είναι απλά λογιστικά θέματα πλέον
η παραγωγή των αντίστοιχων Φυσικών Νόμων
που υπακούουν τα Φυσικά Σώματα που "βλασταίνουν" μέσα σε αυτόν
με δενδροειδείς συνέπειες στην Χημεία, στην Βιολογία,
στην Οικονομία, στην Κοινωνιολογία και γενικά
σε όλες τις Επιστήμες που προκύπτουν με βάση τις προηγούμενες.
------------------
Υπενθυμίζουμε λοιπόν και πάλι
ότι ένας Χώρος αποτελείται από ένα σύνολο σημείων.
Όμως, ο Χώρος δεν είναι "σκορποχώρι"
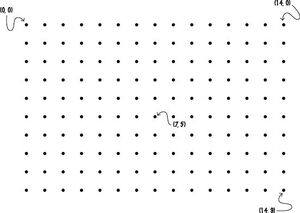 |
| Από την στιγμή που θα ορίσουμε με την βοήθεια των Διαστάσεων ένα σημείο ως αρχή (0,0) τότε κάθε σημείο του Χώρου μπορεί να ταυτοποιηθεί και να λάβει ένα "όνομα" π.χ. (7,9) σε σχέση με την ορισθείσα αρχή |
 |
| Κάθε σημείο του Χώρου π.χ το (2,3,5) καθορίζεται απόλυτα από τις αποστάσεις του (ή αλλιώς συνιστώσες) από τις Διαστάσεις του σχηματίζουν τον Χώρο αυτόν. |
Τα σημεία του κάθε Χώρου υπακούουν σε απαρέγκλιτους κανόνες
"ιεραρχίας" και "κοινωνικής συμπεριφοράς"
α) Η "ιεραρχία" εκφράζεται από
τα δύο διανύσματα της μετατόπισης (ή διανύσματα θέσης)
(ανταλλοίωτο και συναλλοίωτο)
που καθορίζουν, επακριβέστατα, την θέση ενός σημείου του Χώρου
β) Η "κοινωνική συμπεριφορά" εκφράζεται από
την μήτρα απειροστής στροφής
που καθορίζει τον "τρόπο σύνδεσης" των σημείων του
με τα γειτονικά τους
 |
| Ένα φαντασμαγορικό (απλοποιημένο βέβαια) μοντέλο Χωρόχρονου. ---- Εφόσον ένας Χώρος εμπεριέχει και μία Χρονική Διάσταση τότε ένας "παρατηρητής" (που βρίσκεται εκτός του Χώρου αυτού)" θα τον βλέπει κάπως έτσι. |
Υπενθυμίζουμε ότι στα παραπάνω σχήματα,
τα σημεία, είναι απείρως κοντά (δηλ. "κολλητά") μεταξύ τους
ώστε να μην αφήνουν κενά
εφόσον ο Χώρος δεν νοείται να είναι "τρύπιος"
Αυτά τα δύο μαθηματικά εργαλεία είναι πλήρως αρκετά
ώστε να παράγουν όλες τις ιδιότητες ενός Χώρου
Και, όπως έχουμε αναφέρει, πολλάκις, στα προηγούμενα
η πλήρης κατανόηση του Χώρου οδηγεί
στην πλήρη κατανόηση της Γεωμετρίας του
(δηλ. των ιδιοτήτων των Γεωμετρικών Σχημάτων
που "φύονται" μέσα σε αυτόν)
ενώ στην συνέχεια
είναι απλά λογιστικά θέματα πλέον
η παραγωγή των αντίστοιχων Φυσικών Νόμων
που υπακούουν τα Φυσικά Σώματα που "βλασταίνουν" μέσα σε αυτόν
με δενδροειδείς συνέπειες στην Χημεία, στην Βιολογία,
στην Οικονομία, στην Κοινωνιολογία και γενικά
σε όλες τις Επιστήμες που προκύπτουν με βάση τις προηγούμενες.
------------------
Στην συνέχεια ανακεφαλαιώνουμε τα όσα αναφέραμε
1) Τετρα-διάστατος 4D-Πραγματικός Χωρόχρονος Minkowski
(τον μελετήσαμε, ήδη, στο Μέρος Ο18l)
α) Τα δύο διανύσματα Μετατόπισης
(ή αλλιώς διανύσματα Θέσης) είναι:
1) Τετρα-διάστατος 4D-Πραγματικός Χωρόχρονος Minkowski
(τον μελετήσαμε, ήδη, στο Μέρος Ο18l)
α) Τα δύο διανύσματα Μετατόπισης
(ή αλλιώς διανύσματα Θέσης) είναι:
 |
| Ανταλλοίωτο (contravariant) Διάνυσμα όπου: τα ερυθρά x,y,z είναι οι 3 διαστάσεις του γνωστού Χώρου το κυανό t είναι ο γνωστός Χρόνος |
και
β) Η μήτρα Απειροστής Περιστροφής είναι:
2) Τετρα-διάστατος 4D-Φανταστικός Χωρόχρονος Minkowski
(τον παρουσιάσαμε στο Μέρος 25)
α) Τα δύο αντίστοιχα διανύσματα Μετατόπισης
(ή αλλιώς διανύσματα Θέσης) είναι:
και
β) Η αντίστοιχη μήτρα Απειροστής Στροφής είναι:
Επομένως, συνοψίζοντας,
καταλήγουμε στην συνύπαρξη δύο τετραδιάστατων Χωροχρόνων
(ενός Πραγματικού και ένός Φανταστικού)
και επομένως σε ύπαρξη 8 διαστάσεων.
-------------------------------------------------------------------
 |
| Συναλλοίωτο (covariant) Διάνυσμα |
β) Η μήτρα Απειροστής Περιστροφής είναι:
 |
| όπου: θ και φ οι συντελεστές του μετασχηματισμού στροφής δηλ. θ = οι γωνίες μεταξύ των αξόνων του Χώρου φ = οι γωνίες μεταξύ ενός άξονα του Χώρου και του άξονα του Χρόνου |
2) Τετρα-διάστατος 4D-Φανταστικός Χωρόχρονος Minkowski
(τον παρουσιάσαμε στο Μέρος 25)
α) Τα δύο αντίστοιχα διανύσματα Μετατόπισης
(ή αλλιώς διανύσματα Θέσης) είναι:
 |
| Ανταλλοίωτο (contravariant) Διάνυσμα όπου: τα καφετί x,y,z είναι τα μήκη κύματος στους 3 άξονες το πράσινο t δηλώνει την περίοδο του κύματος |
και
 |
| Συναλλοίωτο (covariant) Διάνυσμα |
β) Η αντίστοιχη μήτρα Απειροστής Στροφής είναι:
 |
| όπου: θ και φ οι συντελεστές του μετασχηματισμού στροφής δηλ. θ = οι γωνίες μεταξύ των αξόνων του Χώρου φ = οι γωνίες μεταξύ ενός άξονα του Χώρου και του άξονα του Χρόνου |
Επομένως, συνοψίζοντας,
καταλήγουμε στην συνύπαρξη δύο τετραδιάστατων Χωροχρόνων
(ενός Πραγματικού και ένός Φανταστικού)
και επομένως σε ύπαρξη 8 διαστάσεων.
-------------------------------------------------------------------
--------------------------------------------------------------------

Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου