IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο30-

Χωροχρονική Ενοποίηση
(α' μέρος)

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στο προηγούμενο μέρος
καταλήξαμε σε δύο πενταδιάστατους Χωρόχρονους

1) Έναν Πραγματικό Χωρόχρονο
με διάνυσμα Μετατόπισης (ή αλλιώς διάνυσμα Θέσης):

$\vec{r} = \begin{bmatrix} \color{Magenta}{0} \\ \color{Red}{+x} \\ \color{Red}{+y} \\ \color{Red}{+z} \\ \color{Blue}{-t} \end{bmatrix}$

Ανταλλοίωτο (contravariant) Διάνυσμα
όπου:
- το ροζ (0)
είναι η Επίκενη (Null) Διάσταση
του Πραγματικού Χωρόχρονου
- τα ερυθρά (x, y, z)
είναι οι 3 διαστάσεις του γνωστού Χώρου
- το κυανό (t)
είναι ο γνωστός Χρόνος

2) Και έναν Φανταστικό Χωρόχρονο
με διάνυσμα Μετατόπισης (ή αλλιώς διάνυσμα Θέσης):

$\vec{r} = \begin{bmatrix} \color{Magenta}{i0} \\ \color{Brown}{+ix} \\ \color{Brown}{+iy} \\ \color{Brown}{+iz} \\ \color{Green}{-it} \end{bmatrix}$

Ανταλλοίωτο (contravariant) Διάνυσμα
όπου:
- το ροζ (i0)
είναι η Επίκενη (Null) Διάσταση του Φανταστικού Χωρόχρονου
- τα καφετί (ix, iy, iz)
είναι τα μήκη κύματος στους 3 άξονες
- το πράσινο (it)
είναι η περίοδος του κύματος

Όμως ...
ο Φυσικός Χώρος είναι Ένας και Ενιαίος
Δεν μπορούμε να έχουμε άλλο Χώρο εδώ και άλλον Χώρο αλλού.
Η Φυσική χρειάζεται ένα "ενιαίο γήπεδο για να στήσει το σπιτικό της".

Άλλωστε, ας μην ξεχνάμε ότι αυτό ήταν
και το όνειρο του Max Born (όπως είδαμε στο Μέρος O24):
η ενοποίηση του Φασικού Χώρου

Max Born
(1882 - 1970)

Πρέπει, λοιπόν, να ενοποιήσουμε τους δύο 5D-Χωρόχρονους
σε έναν μοναδικό και Ενιαίο

Εντάξει ... αλλά πως?

Μια πρώτη ιδέα είναι να επικολλήσουμε
τα δύο παραπάνω διανύσματα
το ένα κάτω από το άλλο.
Δυστυχώς, δεν δουλεύει! Οδηγεί σε λάθος υπολογισμούς
Παρόμοιο τρόπο, θα δοκίμασε, άλλωστε, και ο Max Born και πολλοί άλλοι ...

Δεν ζητάμε, λοιπόν, ένα απλό "κόλλημα"
Ζητάμε ένα "κούμπωμα" (clink - clunk)

Το μόνο αλάνθαστο εργαλείο
που κατηύθυνε την Ανθρώπινη Φυσική Έρευνα
για Χιλιετίες
και ποτέ δεν έπεσε έξω
είναι η Συμμετρία.

(Θα μπορούσαμε να την αποκαλέσουμε
το "Μυαλό του Δημιουργού")

παραφράζοντας την γνωστή ρήση σε
"Τα πάντα εν συμμετρία εποίησας")

Έχουμε αναφερθεί πολλές φορές έως τώρα
στην απίστευτη συμμετρικότητα που εμφανίζεται, ποικιλότροπα,
στην Φύση και ιδιαίτερα στους Φυσικούς Νόμους
Καιρός, λοιπόν, να ζητήσουμε και πάλι τα φώτα της.

Ας υπενθυμίσουμε τον τρόπο και πάλι
που οδήγησε τα βήματά μας έως τώρα

Η ανάγκη να εντάξουμε τον μετασχηματισμό της Αναστροφής
στον Χωροχρονικό ιστό του Πραγματικού Χώρου
(όπως, ήδη, αναφέραμε στο Μέρος Ο18-6)
μας οδήγησε στην χειρουργική επέμβαση
να επιπροσθέσουμε στις 4 γνωστές Διαστάσεις (x, y, z, t)
του Πραγματικού Χωρόχρονου Minkowski
την Επίκενη (null) Διάσταση (0) του Πραγματικού Χώρου
και να τον μετατρέψουμε σε Χωρόχρονο Anti-Sitter (AdS)
με 5 Διαστάσεις (0, x, y, z, t)
(όπως, ήδη, αναφέραμε στο Μέρος 18-12)

Η απλή Χωρική Αντιστροφή
εκφράσθηκε από την Απειροστή Μήτρα

$\mathcal R ({\color{Magenta}{\chi}})= \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} \\ \color{Magenta}{+\chi_x} & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_y} & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_z} & \cdot & \cdot & \cdot \\ \end{bmatrix}$

Ενώ η ευρύτερη Χωροχρονική Αντιστροφή
εκφράσθηκε, αντίστοιχα, από την Απειροστή Μήτρα

$\mathcal R ({\color{Magenta}{\chi}}, {\color{Cyan}{\chi_t}}) = \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} & \color{Cyan}{+\chi_t}\\ \color{Magenta}{+\chi_x} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_y} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_z} & \cdot & \cdot & \cdot & \cdot \\ \color{Cyan}{-\chi_t} & \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix}$

Επίσης, αντίστοιχα και εντελώς ανάλογα,
πράξαμε και για τον Φανταστικό Χωρόχρονο
προσθέτοντας και σε αυτόν την δική του Επίκενη (null) Διάσταση

Η ανάγκη να εντάξουμε τον μετασχηματισμό της Αντιστροφής
στον Χωροχρονικό ιστό του Φανταστικού Χώρου
(όπως, ήδη, αναφέραμε στο Μέρος Ο18-6)
μας οδήγησε στην χειρουργική επέμβαση
να επιπροσθέσουμε στις 4 γνωστές Διαστάσεις (ix, iy, iz, it)
του Φανταστικού Χωρόχρονου Minkowski
την Επίκενη (null) Διάσταση (i0) του Φανταστικού Χώρου
και να τον μετατρέψουμε σε Χωρόχρονο Anti-Sitter (AdS)
με 5 Διαστάσεις (i0, ix, iy, iz, it)
(όπως, ήδη, αναφέραμε στο Μέρος 18-12)

Ο μετασχηματισμός της Χωρικής Αναστροφής
εκφράσθηκε από την Απειροστή Μήτρα

$\mathcal R ({\color{Magenta}{i\chi}})= \begin{bmatrix} 0 & \color{Magenta}{-i\chi_x} & \color{Magenta}{-i\chi_y} & \color{Magenta}{-i\chi_z} \\ \color{Magenta}{+i\chi_x} & \cdot & \cdot & \cdot \\ \color{Magenta}{+i\chi_y} & \cdot & \cdot & \cdot \\ \color{Magenta}{+i\chi_z} & \cdot & \cdot & \cdot \\ \end{bmatrix}$

Ενώ ο μετασχηματισμός της ευρύτερης Χωροχρονικής Αντιστροφής
εκφράσθηκε, αντίστοιχα, από την Απειροστή Μήτρα

$\mathcal R ({\color{Magenta}{i\chi}}, {\color{Cyan}{i\chi_t}}) = \begin{bmatrix} 0 & \color{Magenta}{-i\chi_x} & \color{Magenta}{-i\chi_y} & \color{Magenta}{-i\chi_z} & \color{Cyan}{+i\chi_t}\\ \color{Magenta}{+i\chi_x} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+i\chi_y} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+i\chi_z} & \cdot & \cdot & \cdot & \cdot \\ \color{Cyan}{-i\chi_t} & \cdot & \cdot & \cdot & \cdot \\ \end{bmatrix}$

-----
Ο Μετασχηματισμός Αντιστροφής λοιπόν
μας οδήγησε να προσθέσουμε δύο νέες (Επίκενες) Διαστάσεις
στον Φασικό Χώρο ( = Πραγματικό + Φανταστικό)

Ο Μετασχηματισμός Αντιστροφής
μετασχηματίζει
ένα Φυσικό Σώμα (π.χ. Άνθρωπο)
στο είδωλό του μέσα στο κάτοπτρο

Μπαίνουμε, τώρα, στον πειρασμό να αναρωτηθούμε
Μήπως, υπάρχει αντίστοιχος μετασχηματισμός
που να μετασχηματίζει "όντα" του Πραγματικού Χώρου
σε "είδωλα" όχι στον καθρέπτη, αλλά στον Φανταστικό Χώρο????

Ουσιαστικά, ζητάμε κάτι απίστευτο
που μόνο σε κινηματογραφικές ταινίες Επιστημονικής Φαντασίας
συναντάς.
Όπως π.χ. στην ταινία "Tron"

Στην ταινία Tron
ο ήρωας
βρίσκει συσκευή
που τον μεταφέρει από τον "δικό μας" Πραγματικό Χωρόχρονο
στον εικονικό Φανταστικό Χρονόχωρο

Ο ήρωας
μετατρέπεται σε "ολόγραμμα"
δηλ. σε "ον" του Φανταστικού Χώρου

- Υπάρχει, όμως, τέτοιος μετασχηματισμός στην Φυσική?
Δηλαδή, υπάρχει μετασχηματισμός που να επιτρέπει (θεωρητικά)
μία τέτοια απίστευτη μετατροπή
και, ακριβέστερα, να προβλέπει ως εφικτή την κατασκευή μιας τέτοιας μηχανής?
- Ναι, υπάρχει!
Είναι ο Μετασχηματισμός Fourier.

$\begin{matrix} f({\color{Brown}{k_1}}) = \int F_x e^{\color{Brown}{ik_1} {\color{Red}{x}}} d{\color{Red}{x}} \\ f({\color{Brown}{k_2}}) = \int F_y e^{\color{Brown}{ik_2} {\color{Red}{y}}} d{\color{Red}{y}} \\ f({\color{Brown}{k_3}}) = \int F_z e^{\color{Brown}{ik_3} {\color{Red}{z}}} d{\color{Red}{z}} \\ f({\color{Green}{\omega}}) = \int F_t e^{\color{Green}{i\omega} {\color{Blue}{t}}} d{\color{Blue}{t}} \end{matrix}$

Χωρίς να μας ενδιαφέρει
η ακριβής κατανόηση των εξισώσεων
απλά βλέπουμε ξεκάθαρα
πως
οι διαστάσεις του Φανταστικού Χώρου (x, y, z, t)
προκύπτουν
από τις διαστάσεις του Πραγματικού Χώρου (x, y, z, t)

Joseph Fourier
(1768 - 1830)
Διάσημος Γάλλος φυσικός και μαθηματικός
Ούτε που θα το φανταζόταν
ότι οι περίφημοι μετασχηματισμοί του
θα ήταν ο βασικός κρίκος
για την Ενοποίηση
του Ενιαίου Χώρου

Ας δούμε μερικά σχήματα για να αντιληφθούμε
τι ακριβώς κάνουν οι μετασχηματισμοί Fourier

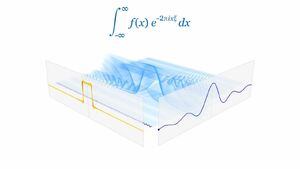Στο εσωτερικό ένας κυματοσυρμός
- Από την δεξιά πλευρά
η προβολή του στον Πραγματικό Χώρο (x,y,z)
- Από την αριστερή πλευρά
η μετασχηματισμένη απεικόνισή του
στον k-Χώρο (k1, k2, k3)
(δηλ. ισοδύναμα, στον Φανταστικό Χώρο (ix, iy, iz))

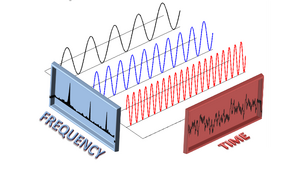Στο εσωτερικό ένας κυματοσυρμός
- Από την δεξιά πλευρά
η προβολή του στον Πραγματικό Χρόνο (t)
- Από την αριστερή πλευρά
η μετασχηματισμένη απεικόνισή του
στον άξονα συχνοτήτων (ω)
(δηλ. ισοδύναμα, στον Φανταστικό Χρόνο (it))

Οπότε?
Οπότε, όπως ο καθένας αντιλαμβάνεται,
χρειαζόμαστε μια νέα Επίκενη (null) Διάσταση
ώστε και αυτός ο μετασχηματισμός
να συμπεριληφθεί στον Χωροχρονικό ιστό.

Ποιά είναι αυτή?
Η Επίκενη (null) Διάσταση του Χρόνου (0).
(αφού ο Χώρος έχει Επίκενη Διάσταση, λογικό δεν είναι
για λόγους συμμετρίας να έχει και ο Χρόνος?)

Ακολουθώντας την ίδια λογική με τον μετασχηματισμό της Αντιστροφής
έχουμε:

Ο Χρονικός Μετασχηματισμός Fourier
θα εκφράζεται από την Απειροστή Μήτρα

$\mathcal R ({\color{Cyan}{\chi_t}}, {\color{Cyan}{i\chi_t}}) = \begin{bmatrix} \color{Cyan}{-\chi_t} \\ 0 \\ \color{Cyan}{+ i\chi_t} \\ \end{bmatrix}$

Ας ενσωματώσουμε και τον Χωρικό Μετασχηματισμό Fourier
οπότε θα λάβουμε τον Χωροχρομικό Μετασχηματισμό Fourier.
(Εδώ θέλει την μέγιστη προσοχή.
Το τμήμα που αφορά τον Φανταστικό Χώρο
επικολλάται ανεστραμμένο ως προς την σειρά των διαστάσεων!
δηλ. όχι x, y, z, t αλλά αντίστροφα t, z, y, x)
Έτσι η Απειροστή Μήτρα γίνεται:

$\mathcal R ({\color{Magenta}{\chi}}, {\color{Cyan}{\chi_t}}, {\color{Magenta}{i\chi}}, {\color{Cyan}{i\chi_t}}) = \begin{bmatrix} \color{Magenta}{+\chi_x} \\ \color{Magenta}{+\chi_y} \\ \color{Magenta}{+\chi_z} \\ \color{Cyan}{-\chi_t} \\ 0 \\ \color{Cyan}{+ i\chi_t} \\ \color{Magenta}{-i\chi_z} \\ \color{Magenta}{-i\chi_y} \\ \color{Magenta}{-i\chi_x} \\ \end{bmatrix}$

Ας ενσωματώσουμε, τώρα, σε αυτήν την μήτρα και την Αντιστροφή

1) Πρώτα ενσωματώνουμε
τον μετασχηματισμό της Χωρικής Αντιστροφής
του Πραγματικού Χωρόχρονου και του Φανταστικού Χρονόχωρου
(που την έχουμε γράψει ήδη παραπάνω)
Έχουμε:

$\mathcal R ({\color{Magenta}{\chi}}, {\color{Cyan}{\chi_t}}, {\color{Magenta}{i\chi}}, {\color{Cyan}{i\chi_t}}) = \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} \\ \color{Magenta}{+\chi_x} & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_y} & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_z} & \cdot & \cdot & \cdot \\ \color{Cyan}{-\chi_t} & \cdot & \cdot & \cdot \\ 0 & 0 & 0 & 0 \\ \color{Cyan}{+ i\chi_t} & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_z} & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_y} & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_x} & \cdot & \cdot & \cdot \\ 0 & \color{Magenta}{+i\chi_x} & \color{Magenta}{+i\chi_y} & \color{Magenta}{+i\chi_z} \\ \end{bmatrix}$

2) Μετά ενσωματώνουμε και
τον μετασχηματισμό της Χρονικής Αναστροφής
του Πραγματικού Χωρόχρονου και του Φανταστικού Χρονόχωρου
(που την έχουμε γράψει ήδη παραπάνω)
Έχουμε:

$\mathcal R ({\color{Magenta}{\chi}}, {\color{Cyan}{\chi_t}}, {\color{Magenta}{i\chi}}, {\color{Cyan}{i\chi_t}}) = \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} & \color{Cyan}{+\chi_t}\\ \color{Magenta}{+\chi_x} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_y} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{+\chi_z} & \cdot & \cdot & \cdot & \cdot \\ \color{Cyan}{-\chi_t} & \cdot & \cdot & \cdot & \cdot \\ 0 & 0 & 0 & 0 & 0 \\ \color{Cyan}{+ i\chi_t} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_z} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_y} & \cdot & \cdot & \cdot & \cdot \\ \color{Magenta}{-i\chi_x} & \cdot & \cdot & \cdot & \cdot \\ 0 & \color{Magenta}{+i\chi_x} & \color{Magenta}{+i\chi_y} & \color{Magenta}{+i\chi_z} & \color{Cyan}{-i\chi_t}\\ \end{bmatrix}$

Ας "γεμίσουμε" τώρα σε αυτήν την μήτρα
ενσωματώνοντας διαδοχικά
τους προηγούμενους μετασχηματισμούς που μελετήσαμε

Αρχίζουμε με την ενσωμάτωση
του μετασχηματισμού της Χωρικής Περιστροφής
(την είχαμε μελετήσει στο Μέρος Ο18k)

1) Πρώτα, στον Πραγματικό Χωρόχρονο
Έχουμε:

$R_{A}={\begin{bmatrix}0&\color {Orange}{-\chi _{x}}&\color {Orange}{-\chi _{y}}&\color {Orange}{-\chi _{z}}&\color {Orange}{+\psi }\\\color {Orange}{-\chi _{x}}&0&\color {Red}{+\theta _{z}}&\color {Red}{-\theta _{y}}&\color {Orange}{+\phi _{x}}\\\color {Orange}{-\chi _{y}}&\color {Red}{-\theta _{z}}&0&\color {Red}{+\theta _{x}}&\color {Orange}{+\phi _{y}}\\\color {Orange}{-\chi _{z}}&\color {Red}{+\theta _{y}}&\color {Red}{-\theta _{x}}&0&\color {Orange}{+\phi _{z}}\\\color {Orange}{-\psi }&\color {Orange}{-\phi _{x}}&\color {Orange}{-\phi _{y}}&\color {Orange}{-\phi _{z}}&0\\\end{bmatrix}}$

Προσθήκη λεζάντας

2) Μετά, στον Φανταστικό Χρονόχωρο
(με προσοχή γιατί είναι ανεστραμμένη)
Θα έχουμε:

$R_{B}={\begin{bmatrix}\color {Cyan}{+\psi }&\color {Cyan}{+\phi _{x}}&\color {Cyan}{+\phi _{y}}&\color {Cyan}{+\phi _{z}}&0\\\color {Cyan}{-\chi _{z}}&\color {Blue}{+\theta _{y}}&\color {Blue}{-\theta _{x}}&0&\color {Cyan}{-\phi _{y}}\\\color {Cyan}{-\chi _{y}}&\color {Blue}{-\theta _{z}}&0&\color {Blue}{+\theta _{x}}&\color {Cyan}{-\phi _{y}}\\\color {Cyan}{-\chi _{x}}&0&\color {Blue}{+\theta _{z}}&\color {Blue}{-\theta _{y}}&\color {Cyan}{-\phi _{x}}\\0&\color {Cyan}{+\chi _{x}}&\color {Cyan}{+\chi _{y}}&\color {Cyan}{+\chi _{z}}&\color {Cyan}{-\psi }\end{bmatrix}}$

Προσθήκη λεζάντας

-------
Συνεχίζουμε ενσωματώνοντας και
τον μετασχηματισμό της Χρονικής Προώθησης
(την είχαμε μελετήσει στο Μέρος Ο18l)

1) Πρώτα, στον Πραγματικό Χωρόχρονο

Προσθήκη λεζάντας

2) Μετά, στον Φανταστικό Χρονόχωρο
(με λίγη προσοχή, γιατί είναι ανεστραμμένη)

Προσθήκη λεζάντας

Αφού, ολοκληρώσαμε την Μήτρα Απειροστής Στροφής,
ενσωματώνοντας όλους τους μετασχηματισμούς,
γράφουμε, τώρα, το Διάνυσμα Μετατόπισης (ή αλλιώς Θέσης)
του Ενιαίου 11-διάστατου Χωρόχρονου

$\vec{r} = \begin{bmatrix} \color{Magenta}{0}\\ \color{Red}{+x} \\ \color{Red}{+y} \\ \color{Red}{+z} \\ \color{Blue}{-t} \\ \color{Cyan}{0} \\ \color{Green}{+it} \\ \color{Brown}{-iz} \\ \color{Brown}{-iy} \\ \color{Brown}{-ix} \\ \color{Magenta}{i0} \end{bmatrix}$

όπου:
το ροζ (0) = η Επίκενη Διάσταση του Πραγματικού Χώρου
τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου
το γαλάζιο (t) = η Διάσταση του Πραγματικού Χρόνου
το κυανό (0) = η Επίκενη Διάσταση του Πραγματικού Χρόνου
το πράσινο (it) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος)
τα καφετί (iz, iy, ix) οι Διαστάσεις του Φανταστικού Χώρου
(ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος)
το ροζ (i0) = η Επίκενη Διάσταση του Φανταστικού Χώρου

--------
Εδώ, μάλλον, ακούσατε όλοι τον "ήχο clink"
H επικόλληση των δύο Χωρόχρονων (Πραγματικού και Φανταστικού)
.... "κούμπωσε"!

ΕΠΙΛΟΓΟΣ :
Όπως, βλέπουμε το όνειρο του Born ολοκληρώθηκε
Ο "Φασικός Χώρος του" ενοποιήθηκε, επιτέλους, συμπεριλαμβάνοντας
και όλες της συμμετρίες της Χορδοθεωρίας.

- όμως...
- τι όμως?
- clunk, δεν ακούστηκε
- ε .. εντάξει ...ασήμαντο, η περισσότερη δουλειά έγινε
- κι όμως, αν δεν ακουστεί κι ο "ήχος clunk",
ποτέ δεν μπορεί να είναι σίγουρος κάποιος
ότι τέλειωσε κάτι,
ειδικά στην Φυσική.

Η συνέχεια στο επόμενο....

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------