IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-Ο37-

Χωροχρονική Ενοποίηση
(η' μέρος)

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στο προηγούμενο μέρος καταλήξαμε τελικά
στην πλήρη μορφή της Μήτρας Απειροστής Στροφής
στον 11-διάστατο Ενιαίο Χωρόχρονο.

$\mathcal R = \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} & \color{Cyan}{+\psi} & 0 & \color{Cyan} i\tilde {\psi}^{-1} & \color{Magenta} i\tilde {\chi}_z^{+1} & \color{Magenta} i\tilde {\chi}_y^{+1} & {\color{Magenta} i\tilde {\chi}_x^{+1}} \; \; \; 0 \\ \color{Magenta}{+\chi_x} & 0 & \color{Red}{+\theta_z} & \color{Red}{-\theta_y} & \color{Blue}{+\phi_x} & 0 & \color{Green} i\tilde {\phi}_x^{-1} & \color{Brown} {i\tilde \theta}_y^{-1} & \color{Brown} {i\tilde \theta}_z^{+1} & 0 \;\; \; \; \color{Magenta} i\tilde {\chi}_x^{-1} \\ \color{Magenta}{+\chi_y} &\color{Red}{-\theta_z} & 0 & \color{Red}{+\theta_x} & \color{Blue}{+\phi_y} & 0 & \color{Green} i\tilde {\phi}_y^{-1} & \color{Brown} {i\tilde \theta}_x^{+1} & 0 & \color{Brown} {i\tilde \theta}_z^{-1} \; \; \; \; \color{Magenta} i\tilde{\chi}_y^{-1} \\ \color{Magenta}{+\chi_z} &\color{Red}{+\theta_y} & \color{Red}{-\theta_x} & 0 & \color{Blue}{+\phi_z} & 0 & \color{Green} i\tilde {\phi}_z^{-1} & 0 & \color{Brown} {i\tilde \theta}_x^{-1} & \color{Brown} {i\tilde \theta}_y^{+1} \; \; \; \color{Magenta} i\tilde{\chi}_z^{-1} \\ \color{Cyan}{-\psi} & \color{Blue}{-\phi_x} & \color{Blue}{-\phi_y} & \color{Blue}{-\phi_z} & 0 & 0 & 0 & \color{Green} i\tilde {\phi}_z^{+1} & \color{Green} i\tilde {\phi}_y^{+1} & \color{Green} i\tilde {\phi}_x^{+1} \; \; \; \color{Cyan} i\tilde {\psi}^{+1} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \; \; \; \; \; \; \; 0 \\ \color{Cyan}{+ i\psi} & \color{Green}{+i\phi_x} & \color{Green}{+i\phi_y} & \color{Green}{+i\phi_z} & 0 & 0 & 0 & \color{Blue} \tilde{\phi}_z^{-1} & \color{Blue} \tilde{\phi}_y^{-1} & \color{Blue} \tilde{\phi}_z^{-1} \; \; \; \color{Cyan} \tilde {\psi}^{-1} \\ \color{Magenta}{-i\chi_z} & \color{Brown}{+i\theta_y} & \color{Brown}{-i\theta_x} & 0 & \color{Green}{-i\phi_z} & 0 & \color{Blue} \tilde{\phi}_z^{+1} & 0 & \color{Red} \tilde {\theta}_x^{-1} & \color{Red} \tilde {\theta}_y^{+1} \; \; \; \color{Magenta} \tilde{\chi}_z^{+1} \\ \color{Magenta}{-i\chi_y} & \color{Brown}{-i\theta_z} & 0 & \color{Brown}{+i\theta_x} & \color{Green}{-i\phi_y} & 0 & \color{Blue} \tilde{\phi}_y^{+1} & \color{Red} \tilde {\theta}_x^{+1} & 0 & \color{Red} \tilde {\theta}_z^{-1} \; \; \; \color{Magenta} \tilde{\chi}_y^{+1} \\ \color{Magenta}{-i\chi_x} & 0 & \color{Brown}{+i \theta_z} & \color{Brown}{-i \theta_y} & \color{Green}{-i\phi_x} & 0 & \color{Blue} \tilde{\phi}_x^{+1} & \color{Red} \tilde {\theta}_y^{-1} & \color{Red} \tilde {\theta}_z^{+1} & 0 \; \; \; \; \; \color{Magenta} \tilde{\chi}_x^{+1} \\ 0 & \color{Magenta}{+i\chi_x} & \color{Magenta}{+i\chi_y} & \color{Magenta}{+i\chi_z} & \color{Cyan}{-i\psi} & 0 & \color{Cyan} \tilde {\psi}^{+1} & \color{Magenta} \tilde{\chi}_z^{-1} & \color{Magenta} \tilde{\chi}_y^{-1} & {\color{Magenta} \tilde{\chi}_x^{-1}} \; \; \; \; 0 \\ \end{bmatrix}$

Αναλυτική (όχι συνοπτική) Μήτρα
Απειροστής Στροφής
του Ενιαίου 11-διάστατου Χωρόχρονου
όπου:
θx, θy, θz = Πραγματική Χωρική Περιστροφή
φx, φy, φz = Πραγματική Χρονική Προώθηση
χx, χy, χz = Πραγματική Χωρική Αντιστροφή
ψ = Πραγματική Χρονική Αναστροφή
και
iθx, iθy, iθz = Φανταστική Χωρική Περιστροφή
iφx, iφy, iφz = Φανταστική Χρονική Προώθηση
iχx, iχy, iχz = Φανταστική Χωρική Αντιστροφή
iψ = Φανταστική Χρονική Αναστροφή
και
οι αντίστοιχες πραγματικές γωνίες
με περισπωμένη (~)
οι Συμπαραγματικές Στροφές
(Περιστροφή, Προώθηση, Αντιστροφή, Αναστροφή)
και
οι αντίστοιχες φανταστικές γωνίες
με περισπωμένη (~)
οι Συμφανταστικές Στροφές
(Περιστροφή, Προώθηση, Αντιστροφή, Αναστροφή)

Όμως, δεν αρκεί απλά η αναγραφή της Μήτρας αυτής
Για την κατανόηση της Κοσμικής Δημιουργίας
απαιτείται η πλήρης και διεξοδική κατανόησή της.

Ας δούμε λοιπόν, αναλυτικότερα, πως αναλύεται ειδικότερα αυτή.

Τα πρώτα που πρέπει να παρατηρήσουμε είναι:
- η μία (κάθετη) στήλη με μηδενικά
- η μία (οριζόντια) σειρά με μηδενικά

Αυτές χωρίζουν τον 11-διάστατο Ενιαίο Χωρόχρονο
σε τέσσερεις 5-διάστατους Χωρόχρονους.

- Δύο από αυτούς είναι τύπου anti-deSitter και
- Δύο υπόλοιποι είναι τύπου deSitter

------
Έτσι έχουμε:
Α) "Φωτεινή Πλευρά"
(ή ακριβέστερα, το "Ηλεκτρογόνο" τμήμα του Ενιαίου Χωρόχρονου)
Διακρίνουμε:
Α1) Πραγματικός πεντα-διάστατος Χωρόχρονος
Είναι ο Χωρόχρονος που ζούμε εμείς.
Είναι, όπως έχουμε αναφέρει, τύπου "anti-deSitter"
"Φιλοξενεί" την Συνήθη (ή αλλιώς Ηλεκτρογενή) Ύλη

$\mathcal R_{real} = \begin{bmatrix} 0 & \color{Magenta}{-\chi_x} & \color{Magenta}{-\chi_y} & \color{Magenta}{-\chi_z} & \color{Cyan}{+\psi} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \cdot \\ \color{Magenta}{+\chi_x} & 0 & \color{Red}{+\theta_z} & \color{Red}{-\theta_y} & \color{Blue}{+\phi_x} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \color{Brown} {\cdot} & \cdot \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{+\chi_y} & \color{Red}{-\theta_z} & 0 & \color{Red}{+\theta_x} & \color{Blue}{+\phi_y} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \cdot & \color{Brown} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{+\chi_z} & \color{Red}{+\theta_y} & \color{Red}{-\theta_x} & 0 & \color{Blue}{+\phi_z} & 0 & \color{Green} {\cdot} & \cdot & \color{Brown} {\cdot} & \color{Brown} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Cyan}{-\psi} & \color{Blue}{-\phi_x} & \color{Blue}{-\phi_y} & \color{Blue}{-\phi_z} & 0 & 0 & \cdot & \color{Green} {\cdot} & \color{Green} {\cdot} & \color{Green} {\cdot} \; \; \; \color{Cyan} {\cdot} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \; \; \; 0 \\ \color{Cyan}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \cdot & 0 & \cdot & \color{Blue} {\cdot} & \color{Blue} {\cdot} & \color{Blue} {\cdot} \; \; \; \color{Cyan} {\cdot} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \color{Red} {\cdot} & \cdot \; \; \; \; \color{Magenta} {\cdot} \\ \cdot & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Cyan}{\cdot} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \cdot \\ \end{bmatrix}$

Α2) Φανταστικός πεντα-διάστατος Χωρόχρονος
Είναι, όπως έχουμε αναφέρει, τύπου "anti-deSitter"
Διαρρέεται από την Ηλεκτρομαγνητική Ακτινοβολία

$\mathcal R_{imag} = \begin{bmatrix} \cdot & \color{Magenta}{\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & \color{Cyan} {\cdot} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \cdot \\ \color{Magenta} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \color{Brown} {\cdot} & \cdot \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \cdot & \color{Brown} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \color{Red}{\cdot} & \cdot & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \cdot & \color{Brown} {\cdot} & \color{Brown} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Cyan}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \cdot & 0 & \cdot & \color{Green} {\cdot} & \color{Green} {\cdot} & \color{Green} {\cdot} \; \; \; \color{Cyan} {\cdot} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \; \; \; 0 \\ \color{Cyan}{+ i\psi} & \color{Green}{+i\phi_x} & \color{Green}{+i\phi_y} & \color{Green}{+i\phi_z} & 0 & 0 & \cdot & \color{Blue} {\cdot} & \color{Blue} {\cdot} & \color{Blue} {\cdot} \; \; \; \color{Cyan} {\cdot} \\ \color{Magenta}{-i\chi_z} & \color{Brown}{+i\theta_y} & \color{Brown}{-i\theta_x} & 0 & \color{Green}{-i\phi_z} & 0 & \color{Blue} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{-i\chi_y} & \color{Brown}{-i\theta_z} & \cdot & \color{Brown}{+i\theta_x} & \color{Green}{-i\phi_y} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta} {-i\chi_x} & 0 & \color{Brown}{+i \theta_z} & \color{Brown}{-i \theta_y} & \color{Green}{-i\phi_x} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \color{Red} {\cdot} & \cdot \; \; \; \color{Magenta} {\cdot} \\ 0 & \color{Magenta}{+i\chi_x} & \color{Magenta}{+i\chi_y} & \color{Magenta}{+i\chi_z} & \color{Cyan}{-i\psi} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \cdot \\ \end{bmatrix}$

Β) "Σκοτεινή Πλευρά"
(ή ακριβέστερα, το Βαρυτογόνο τμήμα του Ενιαίου Χωρόχρονου)
Διακρίνουμε:
Β1) Συμπραγματικός πεντα-διάστατος Χωρόχρονος
Είναι ένας Χωρόχρονος που δεν γίνεται αντιληπτός από εμάς.
Είναι τύπου "deSitter"
"Φιλοξενεί" την Σκοτεινή (ή αλλιώς Βαρυτογενή) Ύλη

$\mathcal R_{co-real} = \begin{bmatrix} \cdot & \color{Magenta}{\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & \color{Cyan} {\cdot} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \; \; \; \; \cdot \\ \color{Magenta} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \color{Brown} {\cdot} & \cdot \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \color{Brown} {\cdot} & \cdot & \color{Brown} {\cdot} \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \color{Red}{\cdot} & \cdot & \color{Blue} {\cdot} & 0 & \color{Green} {\cdot} & \cdot & \color{Brown} {\cdot} & \color{Brown} {\cdot} \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \color{Cyan}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \cdot & 0 & \cdot & \color{Green} {\cdot} & \color{Green} {\cdot} & \color{Green} {\cdot} \; \; \; \; \; \; \; \color{Cyan} {\cdot} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \; \; \; \; \; \; \; 0 \\ \color{Cyan}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \cdot & 0 & 0 & \color{Blue} \tilde{\phi}_z^{-1} & \color{Blue} \tilde{\phi}_y^{-1} & \color{Blue} \tilde{\phi}_z^{-1} \; \; \; \color{Cyan} \tilde {\psi}^{-1} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Green}{\cdot} & 0 & \color{Blue} \tilde{\phi}_z^{+1} & 0 & \color{Red} \tilde {\theta}_x^{-1} & \color{Red} \tilde {\theta}_y^{+1} \; \; \; \color{Magenta} \tilde{\chi}_z^{+1} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} \tilde{\phi}_y^{+1} & \color{Red} \tilde {\theta}_x^{+1} & 0 & \color{Red} \tilde {\theta}_z^{-1} \; \; \; \color{Magenta} \tilde{\chi}_y^{+1} \\ \color{Magenta}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} \tilde{\phi}_x^{+1} & \color{Red} \tilde {\theta}_y^{-1} & \color{Red} \tilde {\theta}_z^{+1} & 0 \; \; \; \; \; \color{Magenta} \tilde{\chi}_x^{+1} \\ \cdot & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Cyan}{\cdot} & 0 & \color{Cyan} \tilde {\psi}^{+1} & \color{Magenta} \tilde{\chi}_z^{-1} & \color{Magenta} \tilde{\chi}_y^{-1} & {\color{Magenta} \tilde{\chi}_x^{-1}} \; \; \; \; 0 \\ \end{bmatrix}$

Β2) Συμφανταστικός πεντα-διάστατος Χωρόχρονος
Είναι τύπου "deSitter"
Διαρρέεται από την Βαρυτική Ακτινοβολία (και την Σκοτεινή Ενέργεια)

$\mathcal R_{co-imag} = \begin{bmatrix} \cdot & \color{Magenta}{\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & \color{Cyan} {\cdot} & 0 & \color{Cyan} i\tilde {\psi}^{-1} & \color{Magenta} i\tilde {\chi}_z^{+1} & \color{Magenta} i\tilde {\chi}_y^{+1} & {\color{Magenta} i\tilde {\chi}_x^{+1}} \; \; \; 0 \\ \color{Magenta} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} i\tilde {\phi}_x^{-1} & \color{Brown} {i\tilde \theta}_y^{-1} & \color{Brown} {i\tilde \theta}_z^{+1} & 0 \; \; \; \; \color{Magenta} i\tilde {\chi}_x^{-1} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Blue} {\cdot} & 0 & \color{Green} i\tilde {\phi}_y^{-1} & \color{Brown} {i\tilde \theta}_x^{+1} & 0 & \color{Brown} {i\tilde \theta}_z^{-1} \; \; \; \; \color{Magenta} i\tilde{\chi}_y^{-1} \\ \color{Magenta} {\cdot} & \color{Red} {\cdot} & \color{Red}{\cdot} & \cdot & \color{Blue} {\cdot} & 0 & \color{Green} i\tilde {\phi}_z^{-1} & 0 & \color{Brown} {i\tilde \theta}_x^{-1} & \color{Brown} {i\tilde \theta}_y^{+1} \; \; \; \color{Magenta} i\tilde{\chi}_z^{-1} \\ \color{Cyan}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \color{Blue}{\cdot} & \cdot & 0 & 0 & \color{Green} i\tilde {\phi}_z^{+1} & \color{Green} i\tilde {\phi}_y^{+1} & \color{Green} i\tilde {\phi}_x^{+1} \; \; \; \color{Cyan} i\tilde {\psi}^{+1} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \; \; \; \; \; \; \; 0 \\ \color{Cyan}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \color{Green}{\cdot} & \cdot & 0 & \cdot & \color{Blue} {\cdot} & \color{Blue} {\cdot} & \color{Blue} {\cdot} \; \; \; \; \; \; \; \color{Cyan} {\cdot} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \cdot & \color{Red} {\cdot} & \color{Red} {\cdot} \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{\cdot} & \color{Brown}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \cdot & \color{Red} {\cdot} \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \color{Magenta}{\cdot} & \cdot & \color{Brown}{\cdot} & \color{Brown}{\cdot} & \color{Green}{\cdot} & 0 & \color{Blue} {\cdot} & \color{Red} {\cdot} & \color{Red} {\cdot} & \cdot \; \; \; \; \; \; \; \color{Magenta} {\cdot} \\ \cdot & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Magenta}{\cdot} & \color{Cyan}{\cdot} & 0 & \color{Cyan} {\cdot} & \color{Magenta} {\cdot} & \color{Magenta} {\cdot} & {\color{Magenta} {\cdot}} \; \; \; \; \; \; \; \cdot \\ \end{bmatrix}$

Για να έχουμε μια εποπτικότερη εικόνα της δομής αυτής
επανερχόμαστε στο "Ιδεογράφημα του Χωρόχρονου"
που εμφανίσαμε στο Μέρος Ο27

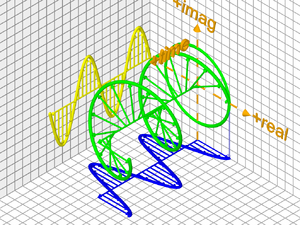Ένα 11-διάστατο Ον
ααποδίδεται από την "πράσινη έλικα"
διαδίδεται στον Ενιαίο 11D-Χωρόχρονο
(στο σχήμα αυτός αντιστοιχεί με το "δωμάτιο")
Έχουμε τώρα:
1) Μία πρώτη προβολή του Όντος,
απεικονίζεται στο "οριζόντιο δάπεδο"
που αντιπροσωπεύει, νοητά, τον 5D-Πραγματικό Χωρόχρονο anti-deSitter
(και αποδίδεται από την γαλάζια συνάρτηση)
2) Μία δεύτερη προβολή του Όντος,
απεικονίζεται στο ένα ζεύγος "παράλληλων τοίχων"
που αντιπροσωπεύει, νοητά, τον 5D-Φανταστικό Χωρόχρονο anti-deSitter
(και αποδίδεται από την κίτρινη συνάρτηση)
3) Μία τρίτη προβολή του Όντος,
απεικονίζεται στην "οριζόντια οροφή"
που αντιπροσωπεύει, νοητά, τον 5D-Συμπραγματικό Χωρόχρονο deSitter
(που δεν διακρίνεται στο σχήμα)
4) Μία τέταρτη προβολή του Όντος,
απεικονίζεται στο άλλο ζεύγος "παράλληλων τοίχων"
που αντιπροσωπεύει, νοητά, τον 5D-Συμφανταστικό Χωρόχρονο deSitter
(που επίσης δεν διακρίνονται στο σχήμα)

-----
Αυτή η ανάλυση πρέπει να είναι αναμενόμενη
γιατί:

Όπως, ακριβώς, ένας Διμιγαδικός Αριθμός (Bicomplex number)

$z = a + ib + \tilde c + i\tilde d$

μπορεί να αναλυθεί σε:
Πραγματικό, Φανταστικό, Συμπραγματικό και Συμφανταστικό τμήμα
εντελώς, παρόμοια, και ο Ενιαίος 11D-Χωρόχρονος
αναλύεται σε:
Πραγματικό, Φανταστικό, Συμπραγματικό και Συμφανταστικό, 5D-Χωρόχρονο

Η συνέχεια στο επόμενο....

-------------------------------------------------------------------
Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------