IonnKorr: Electromagnetism a la Mendeleev

Τετάρτη 28 Σεπτεμβρίου 2016

Electromagnetism a la Mendeleev - A-04

Ηλεκτρομαγνητισμός αλά Mendeleev
-A-04-

Υπερβολοειδή

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Α) Όπως αναφέραμε σε προηγούμενο μέρος,
στον δισ-διάστατο 2D-Χώρο υπάρχει,
μία θεμελιώδης καμπύλη, η Έλλειψη
(που είναι, απλά, ένας γενικευμένος Κύκλος)

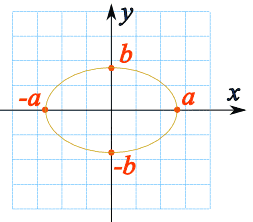Στο σχήμα βλέπουμε
ότι
α = το σημείο που η Έλλειψη τέμνει την Διάσταση (x)
b = το σημείο που η Έλλειψη τέμνει την Διάσταση (y)

Η εξίσωση που περιγράφει την Έλλειψη, στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Επίσης, η εξίσωση της Έλλειψης από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Red}y^{2}}{\color {Red}b^{2}}}=1$

(Υπενθυμίζουμε ότι οι ερυθρές Διαστάσεις (x, y, z) είναι
οι συνήθεις γνωστές πραγματικές διαστάσεις
του Πραγματικού Χώρου της Υπαρκτής Πραγματικότητας).

Τώρα η γενίκευση της Έλλειψης,
στον τρισ-διάστατο 3D-Χώρο,
είναι το Ελλειψοειδές.

Η εξίσωση που περιγράφει το Ελλειψοειδές, στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}+{\frac {z^{2}}{c^{2}}}=1$

Επίσης, η εξίσωση του Ελλειψοειδούς από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Red}y^{2}}{\color {Red}b^{2}}}+{\frac {\color {Red}z^{2}}{\color {Red}c^{2}}}=1$

----------------------------------
Β) Συνεχίζουμε τώρα με μία άλλη θεμελιώδη καμπύλη, την Υπερβολή.

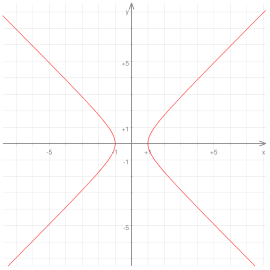Στο σχήμα παρατηρούμε
ότι η Υπερβολή
τέμνει μόνον τον άξονα x (σε δύο σημεία)
αλλά δεν τέμνει σε κανένα σημείο τον άξονα y.

Η εξίσωση που περιγράφει την Υπερβολή, στην Κλασσική Γεωμετρία είναι:

Τώρα, η εξίσωση της Υπερβολής

από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Blue}y^{2}}{\color {Blue}b^{2}}}=1$

[Η εξίσωση αυτή προκύπτει από την κλασσική της μορφή

με χρήση της ταυτότητας i²= -1 οπότε -y²= y²]

Υπενθυμίζουμε ότι οι καστανόχροες Διαστάσεις (x, y, z) είναι

οι πρόσθετες φανταστικές διαστάσεις

(του Φανταστικού Χώρου της Εικονικής Πραγματικότητας).

Ακριβώς αντίστοιχα με την Έλλειψη και το Ελλειψοειδές έχουμε:

ότι η γενίκευση της Υπεροβολής,

στον τρισ-διάστατο 3D-Χώρο,

είναι (όχι ένα αλλά δύο) τα Υπεροβολοειδή.

Βα) Το Μονόχωνο Υπερβολοειδές είναι:

Η εξίσωση που περιγράφει το Μονόχωνο Υπερβολοειδές,
στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1$

Επίσης, η εξίσωση του Μονόχωνου Υπερβολοειδούς

από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Red}y^{2}}{\color {Red}b^{2}}}+{\frac {\color {Blue}z^{2}}{\color {Blue}c^{2}}}=1$

----------------------------------------------------------

Ββ) Το Δίχωνο Υπερβολοειδές είναι:

Η εξίσωση που περιγράφει το Δίχωνο Υπερβολοειδές,

στην Κλασσική Γεωμετρία είναι:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}-{\frac {z^{2}}{c^{2}}}=1$

Επίσης, η εξίσωση του Δίχωνου Υπερβολοειδούς

από την Πολυδιαστατική σκοπιά, γράφεται:

${\frac {\color {Red}x^{2}}{\color {Red}a^{2}}}+{\frac {\color {Blue}y^{2}}{\color {Blue}b^{2}}}+{\frac {\color {Blue}z^{2}}{\color {Blue}c^{2}}}=1$

--------------------------------

Ίσως βαρετά όλα αυτά

αλλά δείχνουν τον τρόπο που οργανώνονται αυτά

τα πολύ θεμελιώδη σχήματα της Γεωμετρίας

στον Ενιαίο 11D-Χωρόχρονο

ενώ οι άμεσες επιπτώσεις στον Άνθρωπο

θα αναλυθούν στο επόμενο μέρος

--------------------------------

ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:

${\vec {r}}={\begin{bmatrix}\color {Red}{q}\\\color {Red}{x}\\\color {Red}{y}\\\color {Red}{z}\\\color {Blue}{t}\\\color {Blue}{e}\\\color {Green}{it}\\\color {Brown}{iz}\\\color {Brown}{iy}\\\color {Brown}{ix}\\\color {Brown}{iq}\end{bmatrix}}$

Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου:
το ερυθρό (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου
τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου
το κυανό (t) = η Διάσταση του Πραγματικού Χρόνου
το κυανό (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου

το πράσινο (it) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος)
τα καστανόχροα (iz, iy, ix) οι Διαστάσεις του Φανταστικού Χώρου
(ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος)
το καστανόχροο (iq) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------