IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-A-06-

Φανταστική Έλλειψη

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Μέχρι τώρα γνωρίσαμε δύο Θεμελιώδη Σχήματα του δισ-διάστατου 2D-Χώρου

(από τα οποία παράγονται όλα τα υπόλοιπα)

Α) την Έλλειψη (δηλ. τον γενικευμένο Κύκλο) (στο Μέρος Α 01):

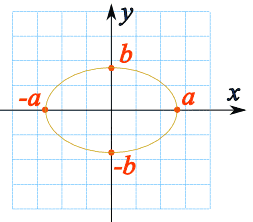Στο σχήμα παρατηρούμε
ότι
η Έλλειψη τέμνει
τόσο τον άξονα της Διάσταση (x)
όσο και τον άξονα της Διάστασης (y)

Η αλγεβρική εξίσωση που περιγράφει την Έλλειψη,
στην Κλασσική Γεωμετρία, είναι:

Β) Την Υπερβολή (στο Μέρος Α-02):

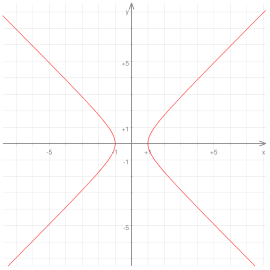Στο σχήμα παρατηρούμε
ότι
η Υπερβολή
τέμνει μόνον τον άξονα της Διάστασης (x)
αλλά δεν τέμνει τον άξονα της Διάστασης (y).

Η αλγεβρική εξίσωση που περιγράφει την Υπερβολή,
στην Κλασσική Γεωμετρία, είναι:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Προσθήκη λεζάντας

Ήρθε λοιπόν ο καιρός να γνωρίσουμε το τρίτο μέλος της παρέας.

Γ) την Φανταστική Έλλειψη.

Η Φανταστική Έλλειψη δεν έχει σχήμα (!)
καθόσον
δεν τέμνει
ούτε τον άξονα της Διάστασης (x)
αλλά ούτε τον άξονα της Διάστασης (y)

Η αλγεβρική εξίσωση που περιγράφει την Φανταστική Έλλειψη,
στην Κλασσική Γεωμετρία, είναι:

$-{\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Προσθήκη λεζάντας

-------------
Είναι εντυπωσιακό αυτό που παρατηρούμε
σε αυτό το απόλυτα θεμελιώδες επίπεδο της Γεωμετρίας και του Χωρόχρονου:
- Χωρίς κανένα μείον, το σχήμα είναι τέλειο (Έλλειψη)
- Με ένα μείον διασπάται και αλλοιώνεται εντυπωσιακά! (Υπερβολή)
- Με δύο μείον εξαφανίζεται εντελώς!! (Φανταστική Έλλειψη)

Τα σχήματα αυτά η Κλασσική Γεωμετρία του 3D-Χώρου αδυνατεί να τα εξηγήσει.
Θεωρεί ότι, απλά, έτσι προκύπτουν από τις εξισώσεις.

Αντίθετα, η Πολυδιαστατική Θεωρία δίνει πολύ ικανοποιητικές εξηγήσεις

Έχουμε λοιπόν:

Α) Η αλγεβρική εξίσωση που περιγράφει την Έλλειψη,
στην Πολυδιαστατική Γεωμετρία, είναι:

Η Έλλειψη "κατοικεί" στην Υπαρκτή Πραγματικότητα.
Οι "ερυθροί" άξονες (x,y) των δύο Διαστάσεων του δισ-διδιάστατου 2D-Χώρου
είναι αμφότεροι "ελκτικοί" και αναγκάζουν την ελαστική καμπύλη
(εδώ υπενθυμίζουμε ότι στην Χορδοθεωρία όλη η Ύλη αποτελείται από "χορδές")
να τμήσει τον καθένα τους σε 2 σημεία του.

Β) Η αλγεβρική εξίσωση που περιγράφει την Υπερβολή,
στην Πολυδιαστατική Γεωμετρία, είναι:

${\color {red}{\frac {x^{2}}{a^{2}}}}+{\color {blue}{\frac {y^{2}}{b^{2}}}}=1$

Προσθήκη λεζάντας

Η Υπερβολή έχει "το ένα πόδι" στην Υπαρκτή Πραγματικότητα
και το άλλο στην Υπαρκτή Πραγματικότητα.
Ο μεν "ερυθρός" άξονας (x) της μίας Διάστασης του πραγματικού δισ-διδιάστατου 2D-Χώρου
είναι "ελκτικός" και αναγκάζει την ελαστική καμπύλη (~ "χορδή")
να τον τμήσει σε 2 σημεία του.

όμως, ο "καστανόχροος" άξονας (y) της άλλης Διάστασης
του φανταστικού δισ-διδιάστατου 2D-Χώρου
είναι "απωστικός" και αναγκάζει την ελαστική καμπύλη (~ "χορδή")
να μην τον τμήσει σε κανένα σημείο του.

Γ) Η αλγεβρική εξίσωση που περιγράφει την Φανταστική Έλλειψη,
στην Πολυδιαστατική Γεωμετρία, είναι:

${\color {blue}{\frac {x^{2}}{a^{2}}}}+{\color {blue}{\frac {y^{2}}{b^{2}}}}=1$

Προσθήκη λεζάντας

Η Φανταστική Έλλειψη "κατοικεί" στην Εικονική Πραγματικότητα.
Οι "γαλάζιοι" άξονες (x,y) των δύο Διαστάσεων
του δισ-διδιάστατου φανταστικού 2D-Χώρου
είναι αμφότεροι "απωστικοί" και απαγορεύουν την ελαστική καμπύλη
να τους τμήσει τους σε οποιοδήποτε σημείο τους.

------------
ΣΥΜΠΕΡΑΣΜΑ:
Η Φανταστική Έλλειψη είναι τόσο υπαρκτή
όσο και οι άλλες καμπύλες.
Απλά δεν ζει στην "Υπαρκτή Πραγματικότητα"
που αντιλαμβάνεται ο άνθρωπος
Δεν μπορούμε να ανιχνεύσουμε την ύπαρξή της
με κανένα τρόπο πλην των Μαθηματικών.
Όμως, υπάρχει στην Επαυξημένη Πραγματικότητα,
αποτελεί και αυτή θεμέλιο των Φυσικών Οντοτήτων
όπως οι άλλες
και οι συνέπειες της "ύπαρξής" της είναι μετρήσιμες
στα Φυσικά Φαινόμενα που συμμετέχει.

Γνωστός αντίστοιχος χαρακτήρας
στην Επιστημονική Φαντασία
ο Αόρατος Άνθρωπος
Όπως στο μυθιστόρημα,
αυτός γίνεται αντιληπτός από την σκιά του
έτσι και η Φανταστική Έλλειψη,
ενώ είναι παντελώς αόρατη,
συμμετέχει
στην οργάνωση και δομή του Σύμπαντος

--------------------------------

ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:

${\vec {r}}={\begin{bmatrix}\color {pink}{q}\\\color {Red}{x}\\\color {Red}{y}\\\color {Red}{z}\\\color {pink}{t}\\e\\\color {cyan}{t}\\\color {blue}{z}\\\color {blue}{y}\\\color {blue}{x}\\\color {cyan}{q}\end{bmatrix}}$

Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου:
το ροδόχροο (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου
τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου
το ροδόχροο (t) = η Διάσταση του Πραγματικού Χρόνου
το μαύρο (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου

το κυανό (t) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος)
τα γλαυκά (z, y, x) οι Διαστάσεις του Φανταστικού Χώρου
(ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος)
το κκυανό (q) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------