IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-A-08-

Ζεύγος Πραγματικών Ευθειών

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Ενδεικτικά, ας αναφέρουμε δύο από τα Θεμελιώδη Σχήματα του δισ-διάστατου 2D-Χώρου

που γνωρίσαμε μέχρι τώρα (από τα οποία παράγονται όλα τα υπόλοιπα)

Α) την Έλλειψη (δηλ. τον γενικευμένο Κύκλο) (στο Μέρος Α 01):

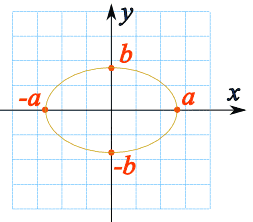Στο σχήμα παρατηρούμε
ότι
η Έλλειψη τέμνει
τόσο τον άξονα της Διάσταση (x)
όσο και τον άξονα της Διάστασης (y)

Η αλγεβρική εξίσωση που περιγράφει την Έλλειψη,
στην Κλασσική Γεωμετρία, είναι:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1$

Προσθήκη λεζάντας

Β) Την Υπερβολή (στο Μέρος Α-02):

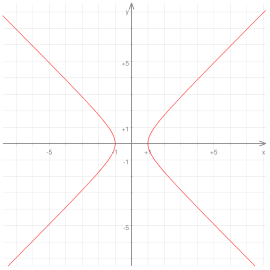Στο σχήμα παρατηρούμε
ότι
η Υπερβολή
τέμνει μόνον τον άξονα της Διάστασης (x)
αλλά δεν τέμνει τον άξονα της Διάστασης (y).

Η αλγεβρική εξίσωση που περιγράφει την Υπερβολή,
στην Κλασσική Γεωμετρία, είναι:

${\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1$

Προσθήκη λεζάντας

Ήρθε λοιπόν ο καιρός να γνωρίσουμε άλλο ένα θεμελιώδες δισδιάστατο σχήμα:

Το Ζεύγος Παραλλήλων Ευθειών

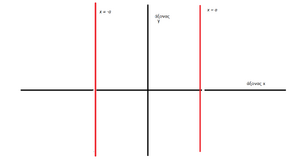Στο σχήμα βλέπουμε
τον άξονα (x) να τέμνεται σε δύο σημεία
αλλά
τον άξονα (t) να μην τέμνεται πουθενά

Η αλγεβρική εξίσωση που περιγράφει tο Ζεύγος Παραλλήλων Ευθειών
στην Κλασσική Γεωμετρία, είναι:

-------------

Όπως έχουμε προαναφέρει, η Πολυδιαστατική Θεωρία
δίνει μία ενιαία μορφή των εξισώσεων αυτών.
Έχουμε λοιπόν:

Α) Η αλγεβρική εξίσωση που περιγράφει την Έλλειψη,
στην Πολυδιαστατική Γεωμετρία, είναι:

${\frac {\color {red}x^{2}}{\color {red}a^{2}}}+{\frac {\color {red}y^{2}}{\color {red}b^{2}}}=1$

Προσθήκη λεζάντας

Οι "ερυθροί" άξονες (x,y) των δύο Διαστάσεων του δισ-διδιάστατου 2D-Χώρου
είναι αμφότεροι "ελκτικοί" και αναγκάζουν την ελαστική καμπύλη
(εδώ υπενθυμίζουμε ότι σύμφωνα με την Χορδοθεωρία όλη η Ύλη αποτελείται από "χορδές")
να τμήσει τον καθένα τους σε 2 σημεία του.

Β) Η αλγεβρική εξίσωση που περιγράφει την Υπερβολή,
στην Πολυδιαστατική Γεωμετρία, είναι:

${\frac {\color {red}x^{2}}{\color {red}a^{2}}}+{\frac {\color {blue}y^{2}}{\color {blue}b^{2}}}=1$

Προσθήκη λεζάντας

Ο μεν "ερυθρός" άξονας (x) της μίας Διάστασης του πραγματικού δισ-διδιάστατου 2D-Χώρου είναι "ελκτικός" και αναγκάζει την ελαστική καμπύλη (~ "χορδή")
να τον τμήσει σε 2 σημεία του.

όμως, ο "καστανόχροος" άξονας (y) της άλλης Διάστασης
του φανταστικού δισ-διδιάστατου 2D-Χώρου
είναι "απωστικός" και αναγκάζει την ελαστική καμπύλη (~ "χορδή")
να μην τον τμήσει σε κανένα σημείο του.

Γ) Η αλγεβρική εξίσωση που περιγράφει το Ζεύγος Παραλλήλων Ευθειών

στην Πολυδιαστατική Γεωμετρία, είναι:

Ο μεν "ερυθρός" άξονας (x)
της μίας Διάστασης του πραγματικού δισ-διδιάστατου 2D-Χώρου
είναι "ελκτικός" και αναγκάζει την ελαστική καμπύλη (~ "χορδή")
που σε αυτήν την περίπτωση είναι το ζεύγος των δύο ευθειών
να τον τμήσει σε 2 σημεία του.
Ο δεύτερος "κυανός" άξονας (t)
της Διάστασης του Χρόνου
δεν έλκει ούτε απωθεί αλλά απαγορεύει στην υλική "χορδή" να τον τμήσει
(ή ισοδύναμα, η τομή γίνεται στο άπειρο)

ΣΥΜΠΕΡΑΣΜΑ:
Συγκρίνοντας τα 3 παραπάνω σχήματα παρατηρούμε ότι
ενώ
οι "ερυθρές" πραγματικές Χωρικές Διαστάσεις
έλκουν τα άκρα μίας "χορδής" και απωθούν το μέσο του
και οι "καστανόχροοες" φανταστικές Χωρικές Διαστάσεις
απωθούν τα άκρα μιας "χορδής" και έλκουν το μέσο του
αντίθετα
η "γαλάζια" Χρονική Διάσταση ούτε έλκει ούτε απωθεί,
απλά απαγορεύει στην χορδή να την τμήσει, αναγκάζοντάς την
να μείνει σε παράλληλη θέση.

Από αυτήν την διαφορά Χώρου και Χρόνου
ξεκινούν όλες οι υπόλοιπες διαφορές τους
που τους καθιστούν τελείως διαφορετικές οντότητες
του Σύμπαντος.

--------------------------------

ΣΗΜΕΙΩΣΗ:
Υπενθυμίζουμε ότι
το Διάνυσμα Θέσης του 11D-Χωρόχρονου
είναι:

${\vec {r}}={\begin{bmatrix}\color {pink}{q}\\\color {Red}{x}\\\color {Red}{y}\\\color {Red}{z}\\\color {pink}{t}\\e\\\color {cyan}{t}\\\color {blue}{z}\\\color {blue}{y}\\\color {blue}{x}\\\color {cyan}{q}\end{bmatrix}}$

Ανταλλοίωτο (contravariant) Διάνυσμα Θέσης
όπου:
το ροδόχροο (q) = η Μοναδιαία Διάσταση του Πραγματικού Χώρου
τα ερυθρά (x, y, z) = οι 3 γνωστές Διαστάσεις του Πραγματικού Χώρου
το ροδόχροο (t) = η Διάσταση του Πραγματικού Χρόνου
το μαύρο (e) = η Μοναδιαία Διάσταση του Πραγματικού Χρόνου

το κυανό (t) = η Διάσταση του Φανταστικού Χρόνου
(ή ισοδύναμα, η αντίστροφη συχνότητα, ή η Περίοδος Κύματος)
τα γλαυκά (z, y, x) οι Διαστάσεις του Φανταστικού Χώρου
(ή ισοδύναμα, οι αντίστροφοι κυματάριθμοι, ή τα μήκη Κύματος)
το κκυανό (q) = η Μοναδιαία Διάσταση του Φανταστικού Χώρου

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------