Ηλεκτρομαγνητισμός αλά Mendeleev
-B-06-

B. Ηλεκτροστατική
Ηλεκτρικές Οντότητες
--------------------------------------------------------------------
--------------------------------------------------------------------
Στα προηγούμενα Μέρη
(Μέρος Β-01, Μέρος Β-02, Μέρος Β-03, Μέρος B-04, Μέρος B-05)
Στα προηγούμενα Μέρη
(Μέρος Β-01, Μέρος Β-02, Μέρος Β-03, Μέρος B-04, Μέρος B-05)
αναπτύξαμε μία εκτεταμένη επιχειρηματολογία
προκειμένου να γίνει σαφές ότι υπάρχει απόλυτη αντιστοιχία
Γεωμετρικών και των Φυσικών Μεγεθών.
Υπενθυμίζουμε ότι
αν ο Χώρος δεν είναι κενός αλλά ενσωματώνει
μία (οποιαδήποτε) Φυσική Οντότητα
(όπως π.χ. Ηλεκτρισμός, Βαρύτητα κλπ)
τότε τα Γεωμετρικά Μεγέθη θα πρέπει αντικατασταθούν
με τα αντίστοιχα Φυσικά Μεγέθη.
Πριν παρατεθούν οι σχετικοί πίνακες,
προτάσσεται ένα χαρακτηριστικό παράδειγμα
Στο Μέρος Ο16 της εισαγωγής μελετήσαμε την διαδικασία
της παρατήρησης ενός "γεωμετρικού αντικειμένου"
Κάθε Παρατηρητής διαθέτει δύο Θεάσεις (viewpoints):
- την Μακροσκοπική Θέαση
(παρατήρηση του αντικειμένου, "εξωειδώς", ή αλλιώς, ολικά)
- την Μικροσκοπική Θέαση
(παρατήρηση του αντικειμένου, "εσωειδώς", ή αλλιώς, σημειακά)
Τα μεγέθη που χρησιμοποιούνται για την Μακροσκοπική περιγραφή
αποκαλούνται Εκτατικά Μεγέθη
ενώ αντίστοιχα
Τα μεγέθη που χρησιμοποιούνται για την Μικροσκοπική περιγραφή
αποκαλούνται Εντατικά Μεγέθη
Επομένως,
απαιτούνται δύο πίνακες μεγεθών (γεωμετρικών και φυσικών)
για την περιγραφή από την πλευρά της Μακροσκοπικής Θέασης
και αντίστοιχα άλλοι δύο πίνακες μεγεθών (γεωμετρικών και φυσικών)
για την περιγραφή από την πλευρά της Μικροσκοπικής Θέασης
Πρώτα, ο πίνακας με τα Γεωμετρικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μακροσκοπικά.
Ακολουθεί, ο πίνακας με τα Φυσικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μακροσκοπικά.
Στην συνέχεια, ο πίνακας με τα Γεωμετρικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
Υπενθυμίζουμε ότι
αν ο Χώρος δεν είναι κενός αλλά ενσωματώνει
μία (οποιαδήποτε) Φυσική Οντότητα
(όπως π.χ. Ηλεκτρισμός, Βαρύτητα κλπ)
τότε τα Γεωμετρικά Μεγέθη θα πρέπει αντικατασταθούν
με τα αντίστοιχα Φυσικά Μεγέθη.
Πριν παρατεθούν οι σχετικοί πίνακες,
προτάσσεται ένα χαρακτηριστικό παράδειγμα
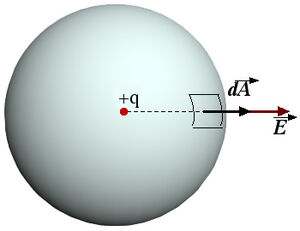 |
| Στο σχήμα ένα παράδειγμα. ----- Πρώτα στην καθαρή Γεωμετρία: α) Το εσωτερικό της Κενής σφαίρας είναι μία τρισδιάστατη (3D) Χωροπεριοχή που περιγράφεται από το γεωμετρικό μέγεθος "Όγκος" (Ω) β) Το ιδεατό περίβλημα είναι μία δισδιάστατη (2D) Επιφάνεια που περιγράφεται από το γεωμετρικό μέγεθος "Εμβαδό" (Σ) ------ Πάμε τώρα στην Φυσική: Εφόσον η σφαίρα δεν είναι Κενή αλλά είναι πλήρης από μία Φυσική Οντότητα (π.χ. Ηλεκτρικό Φορτίο) τότε α) η τρισδιάστατη (3D) Χωροπεριοχή θα περιγράφεται από το φυσικό μέγεθος "Ολότητα" (Ψ) και β) η δισδιάστατη (2D) Επιφάνεια θα περιγράφεται από το φυσικό μέγεθος "Ροή" (Φ) |
Στο Μέρος Ο16 της εισαγωγής μελετήσαμε την διαδικασία
της παρατήρησης ενός "γεωμετρικού αντικειμένου"
Κάθε Παρατηρητής διαθέτει δύο Θεάσεις (viewpoints):
- την Μακροσκοπική Θέαση
(παρατήρηση του αντικειμένου, "εξωειδώς", ή αλλιώς, ολικά)
- την Μικροσκοπική Θέαση
(παρατήρηση του αντικειμένου, "εσωειδώς", ή αλλιώς, σημειακά)
Τα μεγέθη που χρησιμοποιούνται για την Μακροσκοπική περιγραφή
αποκαλούνται Εκτατικά Μεγέθη
ενώ αντίστοιχα
Τα μεγέθη που χρησιμοποιούνται για την Μικροσκοπική περιγραφή
αποκαλούνται Εντατικά Μεγέθη
Επομένως,
απαιτούνται δύο πίνακες μεγεθών (γεωμετρικών και φυσικών)
για την περιγραφή από την πλευρά της Μακροσκοπικής Θέασης
και αντίστοιχα άλλοι δύο πίνακες μεγεθών (γεωμετρικών και φυσικών)
για την περιγραφή από την πλευρά της Μικροσκοπικής Θέασης
Πρώτα, ο πίνακας με τα Γεωμετρικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μακροσκοπικά.
Ακολουθεί, ο πίνακας με τα Φυσικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μακροσκοπικά.
| Μακροσκοπική Θέαση Φυσική | ||
|---|---|---|
| α/α | Γεωμετρικά Στοιχεία | Φυσικά Μεγέθη |
| 1. | Χωροπεριοχή (Volume) | Ολότητα (Totality) (Ψ) |
| 2. | Επιφάνεια (Surface) | Ροή (Flux) (Φ) |
| 3. | Καμπύλη (curve) | Ρύση (Flow) (Γ) |
| 4. | Σημείο (Point) | Τάση (Tension) (Τ) |
Στην συνέχεια, ο πίνακας με τα Γεωμετρικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μικροσκοπικά.
Και ακολουθεί, ο πίνακας με τα Φυσικά μεγέθη
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μικροσκοπικά.
που χρησιμοποιεί ο Παρατηρητής που παρατηρεί τα αντικείμενα,
μικροσκοπικά.
ΣΥΜΠΕΡΑΣΜΑ (Τι κρατάμε από τους παραπάνω πίνακες):
Ότι ένας Χωροχρονικός Παρατηρητής
αδυνατεί να διακρίνει αυτό που μετράει
σε μία στρεβλωμένη επιφάνεια (ή χωροπεριοχή ή καμπύλη κλπ)
είναι π.χ.
- το γεωμετρικό μέγεθος "Εμβαδόν" (Σ)
ή το φυσικό μέγεθος "Ροή" (Φ)
- το γεωμετρικό μέγεθος "Μήκος Καμπύλης" (Λ)
ή το φυσικό μέγεθος "Ρύση" (Γ)
- το γεωμετρικό μέγεθος "Όγκος" (Ω)
ή το φυσικό μέγεθος "Ολότητα" (Ψ)
- το γεωμετρικό μέγεθος "Ιακωβιανή καμπυλότητα" (J(3)) )
(ή το φυσικό μέγεθος "Πυκνότητα" (Q) )
- κλπ, κλπ.
----
Από το επόμενο, λοιπόν, αρχίζουν να παρατίθενται
οι Πίνακες του Ηλεκτρομαγνητισμού αλά Mendeleev.
-------------------------------------------------------------------
Ότι ένας Χωροχρονικός Παρατηρητής
αδυνατεί να διακρίνει αυτό που μετράει
σε μία στρεβλωμένη επιφάνεια (ή χωροπεριοχή ή καμπύλη κλπ)
είναι π.χ.
- το γεωμετρικό μέγεθος "Εμβαδόν" (Σ)
ή το φυσικό μέγεθος "Ροή" (Φ)
- το γεωμετρικό μέγεθος "Μήκος Καμπύλης" (Λ)
ή το φυσικό μέγεθος "Ρύση" (Γ)
- το γεωμετρικό μέγεθος "Όγκος" (Ω)
ή το φυσικό μέγεθος "Ολότητα" (Ψ)
- το γεωμετρικό μέγεθος "Ιακωβιανή καμπυλότητα" (J(3)) )
(ή το φυσικό μέγεθος "Πυκνότητα" (Q) )
- κλπ, κλπ.
----
Από το επόμενο, λοιπόν, αρχίζουν να παρατίθενται
οι Πίνακες του Ηλεκτρομαγνητισμού αλά Mendeleev.
-------------------------------------------------------------------
--------------------------------------------------------------------
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου