Electromagnetism a la Mendeleev - B-08

Ηλεκτρομαγνητισμός αλά Mendeleev
-B-08-

B. Ηλεκτροστατική
Φυσικοί Νόμοι Σύνδεσης

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------

Στο Μέρος Β 01 είδαμε ότι
η Φυσική Οντότητα "Ηλεκτρομαγνητισμός"
εμφανίζεται στον τρισδιάστατο 3D-Χώρο
με 4 εντελώς διαφορετικά "πρόσωπα"
δηλ. ως να συνίσταται από  4 διακριτές Φυσικές Οντότητες (entities):
- Ηλεκτρικό Φορτίο
- Ηλεκτρικό Ρεύμα
- Μαγνητικό Πεδίο
- Ηλεκτρικό Πεδίο

Επίσης, αναφέραμε, επανειλημμένως, ότι
οι 4 αυτές Φυσικές Οντότητες
σχετίζονται στενότατα με την Γεωμετρία του Χώρου
(δηλ. αλλιώς, μπορούμε να τις μελετήσουμε
ως να ήταν Γεωμετρικές Οντότητες).

Αυτή, ακριβώς, η στενή σχέση
των Ηλεκτρομαγνητικών Οντοτήτων
με τα γεωμετρικά στοιχεία του Χώρου
- επιβάλλει την Γεωμετροποίηση της Φυσικής, και
- καθορίζει, αποκλειστικά και απόλυτα,
  όχι μόνον το είδος των Φυσικών Μεγεθών
  με τα οποία περιγράφει, η Φυσική, τις Φυσικές Οντότητες, αυτές
  αλλά και την υφή των Φυσικών Νόμων
  στους οποίους υπακούουν αυτά τα Μεγέθη.

Διακρίνουμε τρία είδη Φυσικών Νόμων:
  α) Φυσικοί Νόμοι Σύνδεσης
  β) Φυσικοί Νόμοι Διατήρησης
  γ) Πεδιακοί Φυσικοί Νόμοι

Θα αρχίσουμε με την "πινακοποίηση" των πρώτων

Όπως είδαμε,
στο Μέρος Ο16 της εισαγωγής,
όπου μελετήσαμε την δυικότητα της διαδικασίας της παρατήρησης
ενός "γεωμετρικού αντικειμένου",
(επομένως, και της όποιας γεωμετροποιημένης Φυσικής Οντότητας),
κάθε Φυσικός Παρατηρητής διαθέτει δύο "Θεάσεις" (viewpoints):
- την Μακροσκοπική Θέαση
  (παρατήρηση του αντικειμένου, εξωειδώς, ή αλλιώς, ολιστικά,
   που απαιτεί την χρήση Εκτατικών Μεγεθών)
- την Μικροσκοπική Θέαση
  (παρατήρηση του αντικειμένου, εσωειδώς, ή αλλιώς, σημειακά,
   που απαιτεί την χρήση Εντατικών Μεγεθών)

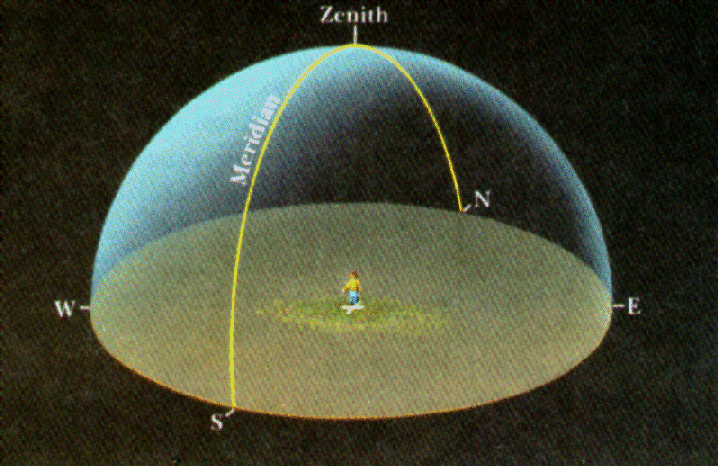Αν θεωρήσουμε π.χ.
ότι η μελετούμενη Οντότητα
είναι ο "κίτρινος" δίσκος
τότε
ο Μακροσκοπικός Παρατηρητής
την παρατηρεί, ως όλον, "απ' έξω"
ενώ
ο Μικροσκοπικός Παρατηρητής
την παρατηρεί, σημείο προς σημείο, "από μέσα"

Η Αρχή της Σχετικότητας (αλλά και η Παγκόσμια Δικαιοσύνη)
απαιτούν να ισχύει ότι
οι δύο αυτοί Φυσικοί Παρατηρητές πρέπει να είναι "ισοδύναμοι"
(δηλ. να περιγράφουν, αμφότεροι, την ίδια "Αλήθεια")

Ωραία... αλλά..
- ο μεν Παρατηρητής με την Μακροσκοπική Θέαση
χρησιμοποιεί, για την περιγραφή του, Εκτατικά Φυσικά Μεγέθη
- ο δε Παρατηρητής με την Μικροσκοπική Θέαση
χρησιμοποιεί, για την περιγραφή του, Εντατικά Φυσικά Μεγέθη

Οπότε?
Οπότε, πρέπει αυτά τα δύο είδη να συνδέονται
με έναν "μηχανισμό ακριβείας"
ώστε να μπορεί ο καθένας τους
να μετατρέπει, πιστοποιημένα,
τα δεδομένα (δηλ. τις μετρήσεις) του άλλου
σε δεδομένα της δικής του θέασης.

Ακριβώς αυτή την διαδικασία της "δίκαιης" μετατροπής
απεικονίζουν οι Νόμοι Σύνδεσης.

Η "ψυχή" των Νόμων Σύνδεσης
(που επωμίζεται το βάρος της μετατροπής)
είναι οι Τελεστές.

Το καλύτερο απτό
παράδειγμα Τελεστή
είναι
ο (ερυθρός) Διωστήρας
μετατρέπει
την Παλινδρομική Κίνηση των εμβόλων
σε
Περιστροφική Κίνηση ενός άξονα
Ακριβώς,
αντίστοιχη μετατροπή
εκτελεί ένας Τελεστής
στην Φυσική
Μετατρέπει μία συνάρτηση (Μέγεθος) σε μία άλλη.

Ψάχνουμε, λοιπόν, έναν τελεστή
που θα "γεωμετροποιεί" Φυσικά Μεγέθη (δηλ. που ως γνωστόν είναι συναρτήσεις)
Αυτός είναι:
                             ο Τελεστής Ολοκλήρωσης (ή απλά, ολοκλήρωμα)
Αυτός, με απλά λόγια,
παίρνει "γυμνά" Εντατικά Φυσικά Μεγέθη (της Μικροσκοπικής Θέσης)
και τα "ντύνει" με γεωμετρικά "κουστούμια"
και τα μετατρέπει
σε "ντυμένα" Εκτατικά Φυσικά Μεγέθη  (της Μακροσκοπικής Θέσης)

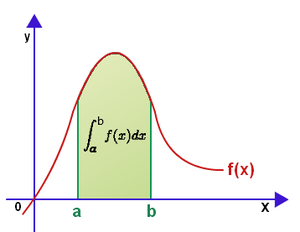Ο Τελεστής της Ολοκλήρωσης
μετατρέπει
ένα Φυσικό Μέγεθος
(στο σχήμα απεικονίζεται από την "ερυθρή" συνάρτηση)
σε
ένα Γεωμετρικό Σχήμα
(στο σχήμα απεικονίζεται από την "πράσινη" επίπεδη περιοχή)

Ακολουθούν, λοιπόν, οι περιβόητοι πίνακες

που θα "αρχειοθετήσουν" τους Φυσικούς Νόμους Σύνδεσης "σε κουτιά"

(όπως έγινε με τα Φυσικά Μεγέθη στο προηγούμενο Μέρος)

Πρώτα, παρουσιάζεται ο πίνακας

των Νόμων Σύνδεσης των Δυναμικών Μεγεθών της Εσωτεριακής Άποψης

(δηλ. αυτών που περιγράφουν το Εσώτερο Τμήμα της κάθε Φυσικής Οντότητας)

Δυναμική Άποψη

Γεωμετροποίηση Ηλεκτροφυσικής Ηλεκτροφυσικοί Νόμοι Σύνδεσης (Πίνακας 1) Εξισώσεις A.01, A.02, A.03, A.04 (3D-Χώρος) Εκτατική Θέαση & Εντατική Θέαση (Εκτατικά Μεγέθη και Εντατικά Μεγέθη) Δυναμική Άποψη (Δυναμικά Μεγέθη)
α/α	Φυσική Οντότητα και αντίστοιχη Γεωμετρική	Φυσικός Νόμος και επισυναπτόμενη Εξίσωση
A.01	Ηλεκτρικό Φορτίο (Electric Charge) Χωροπεριοχή	Νόμος Σύνδεσης Ηλεκτρικού Φορτίου ΨQ=∭dV⋅ Q
A.02	Ηλεκτρικό Ρεύμα (Electric Current) Κυλινδροειδής Επιφάνεια	Νόμος Σύνδεσης Ηλεκτρικού Ρεύματος ΦJ=∬d S   ⃗   ⋅ J⃗
A.03	Μαγνητικό Πεδίο (Magnetic Field) Ανοικτή Επιφάνεια	Νόμος Σύνδεσης Μαγνητικού Πεδίου ΦB=∬d S⃗  ⋅ B⃗
A.04	Ηλεκτρικό Πεδίο (Electric Field) Ανοικτή Καμπύλη	Νόμος Σύνδεσης Ηλεκτρικού Πεδίου ΓE=∫dr⃗ ⋅ E⃗
Εμπλεκόμενα Φυσικά Μεγέθη
Φορτιακή Ολότητα (Charge Totality) (ΨQ) Ρευματική Ροή (Current Flux) (ΦJ) Μαγνητική Ροή (Magnetic Flux) (ΦB) Ηλεκτρική Ρύση (Electric Flow) (ΓE)		Φορτιακή Πυκνότητα (Charge Density) (Q) Ρευματική Πυκνότητα (Current Density) (J) Μαγνητική Ένταση (Magnetic Strength) (B) Ηλεκτρική Ένταση (Electric Strength) (E)
Εμπλεκόμενοι Γεωμετρικός Τελεστές
Επιχώρια Ολοκλήρωση (Volume Integral) Επιφανειακή Ολοκλήρωση (Surface Integral) Επικαμπύλια Ολοκλήρωση (Curve Integral)		∭dV⋅ ∫∫d S⃗  ⋅ ∫dr⃗ ⋅

Δυνητική Άποψη

Γεωμετροποίηση Ηλεκτροφυσικής Ηλεκτροφυσικοί Νόμοι Σύνδεσης (Πίνακας 2) Εξισώσεις A.05, A.06, A.07, A.08 (3D-Χώρος) Εκτατική Θέαση & Εντατική Θέαση (Εκτατικά Μεγέθη & Εντατικά Μεγέθη) Δυνητική Άποψη (Δυνητικά Μεγέθη)
α/α	Φυσική Οντότητα και αντίστοιχη Γεωμετρική	Φυσικός Νόμος και επισυναπτόμενη Εξίσωση
A.05	Ηλεκτρικό Φορτίο (Electric Charge) Κλειστή Επιφάνεια	Νόμος Σύνδεσης Ηλεκτρικού Φορτίου ΦD=∬d S⃗ ⋅ D⃗
A.06	Ηλεκτρικό Ρεύμα (Electric Current) Ζεύγος Κλειστών Καμπυλών	Νόμος Σύνδεσης Ηλεκτρικού Ρεύματος ΓH=∫dr⃗ ⋅ H⃗
A.07	Μαγνητικό Πεδίο (Magnetic Field) Κλειστή Καμπύλη	Νόμος Σύνδεσης Μαγνητικού Πεδίου ΓA=∫dr⃗ ⋅ A⃗
A.08	Ηλεκτρικό Πεδίο (Electric Field) Ζεύγος Σημείων	Νόμος Σύνδεσης Ηλεκτρικού Πεδίου ΠV=1⋅V
Εμπλεκόμενα Φυσικά Μεγέθη
Φορτιακή Ροή (Charge Flux) (ΦD) Ρευματική Ρύση (Current Flow) (ΓH) Μαγνητική Ρύση (Magnetic Flow) (ΓA) Ηλεκτρική Τάση (Electric Tension) (ΠV)		Φορτιακό Δυναμικό (Charge Potential) (D) Ρευματικό Δυναμικό (Current Potential) (H) Μαγνητικό Δυναμικό (Magnetic Potential) (A) Ηλεκτρικό Δυναμικό (Electric Potential) (V)
Εμπλεκόμενοι Γεωμετρικοί Τελεστές
Επιφανειακή Ολοκλήρωση (Surface Integral) Επικαμπύλια Ολοκλήρωση (Curve Integral) Διαφορά (Difference)		∬d S⃗ ⋅ ∫dr⃗ ⋅ Δ⋅

----

Συμπέρασμα:

Ετσι καταλήξαμε λοιπόν, ξεκάθαρα,
σε 4 + 4  = 8 Νόμους Σύνδεσης
που απαιτούνται για την μελέτη του Ηλεκτρομαγνητισμού.

"Αυτό που πρέπει να μας εντυπωσιάζει, υπέρμετρα,

δεν είναι το γεγονός ότι

η Γεωμετροποίηση του Ηλεκτρομαγνητισμού

προσφέρει "στο πιάτο" τους 8 Νόμους Σύνδεσης

που αναδύονται, αυθόρμητα,

μέσα από την γεωμετρικότητα των 4 Οντοτήτων

αλλά ...το γεγονός ότι

 οι επιστήμονες, μέσα από έρευνα αιώνων,

με μόνον πειραματικά και θεωρητικά μέσα,

επέτυχαν να προσδιορίσουν, βαθμιαία,

αυτούς τους 8 νόμους

παρ' ότι αγνοούσαν, παντελώς, την Γεωμετροποίηση!"

Υπενθύμιση:
"Εμείς, οι Άνθρωποι,
δεν θα μπορέσουμε ποτέ να προσεγγίσουμε
την "Δημιουργία του Σύμπαντος"
αν δεν προχωρήσουμε
από την Γνώση στην Κατανόηση της Φυσικής"

Μετά και την ανάγνωση του παρόντος Μέρους, αρχίζουν, προφανώς,
να αντιλαμβάνονται και οι πλέον ανυποψίαστοι αναγνώστες ότι
ο συνδυασμός Γεωμετροποίησης και Πολυδιαστατικής Θεωρίας
είναι ο ευκολότερος (ίσως και ο μοναδικός) δρόμος
να "περάσει" κάποιος από την απλή Γνώση (Knowledge),
στην σύνθετη Κατανόηση (Understanding) του Σύμπαντος.

-------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------