IonnKorr: Electromagnetism a la Mendeleev

Ηλεκτρομαγνητισμός αλά Mendeleev
-B-09-

B. Ηλεκτροστατική
Φυσικοί Νόμοι Διατήρησης

--------------------------------------------------------------------

Εδώ βρίσκουμε τα περιεχόμενα της θεματικής ενότητας

--------------------------------------------------------------------
Όπως αναφέραμε προηγουμένως
διακρίνουμε τρία είδη Φυσικών Νόμων:
α) Φυσικοί Νόμοι Σύνδεσης
β) Φυσικοί Νόμοι Διατήρησης
γ) Πεδιακοί Φυσικοί Νόμοι

Στο προηγούμενο Μέρος Β-08 αναφέραμε τους Φυσικούς Νόμους Σύνδεσης
Στο παρόν Μέρος θα ασχοληθούμε με τους Νόμους Διατήρησης

Τι είναι όμως ένας Νόμος Διατήρησης???

Ουσιαστικά, θα μπορούσε να αποκληθεί ως η "Αρχή του Αυτονόητου"

Ας γίνουμε σαφέστεροι.

Κάθε Γεωμετρικό Σχήμα εγκλείει στο εσωτερικό του μέρος

ένα απόλυτο "ιδεατό" Κενό ("Γεωμετρικό Κενό")

To "γεωμετρικό κενό"
είναι το απόλυτο ιδεατό Κενό
που δεν εμπεριέχει
κανένα είδος Ύλης ή Ενέργειας
ή οποιασδήποτε οντότητας, γενικά

Αν τοποθετηθεί Ύλη ή Ενέργεια μέσα στο γεωμετρικό αυτό σχήμα

(χωρίς άλλη εξωτερική επέμβαση)

αυτή θα παραμείνει ως έχει

(δηλ.

- ούτε θα αυξηθεί με δημιουργία

- ούτε θα μειωθεί με καταστροφή)

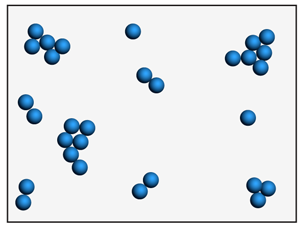Ένα παράδειγμα Διατήρησης
-----
Έστω ότι μέσα σε μία Χωροπεριοχή
π.χ. υπάρχουν 30 σωματίδια
Είναι αυτονόητο
ότι όσες μετρήσεις και να γίνουν,
από οποιουσδήποτε Φυσικούς Παρατηρητές,
ο αριθμός των σωματιδίων θα διατηρηθεί
(δηλ. τα σωματίδια θα εξακολουθήσουν να είναι 30)
Ούτε θα αυξηθούν (δημιουργία Ύλης εκ του μηδενός),
ούτε θα μειωθούν (καταστροφή Ύλης προς το μηδεν)

Οι Φυσικοί Νόμοι Διατήρησης,

(που ουσιαστικά είναι απόρροια του Νόμου Διατήρησης Ύλης-Ενέργειας)

είναι ο ακρογωνιαίος λίθος

όχι μόνον της Φυσικής αλλά και της ίδιας της Λογικής.

Προφανώς, οι Νόμοι Διατήρησης (όπως γενικότερα, οι Φυσικοί Νόμοι)

δεν ισχύουν επιλεκτικά, ανάλογα με τις περιστάσεις,

αλλά ισχύουν σε κάθε σημείο του Σύμπαντος (και του Πολυσύμπαντος)

και σε οποιαδήποτε χρονική στιγμή του Παρελθόντος, του Παρόντος και του Μέλλοντος.

Αν υποτεθεί ότι, κάπου ή κάποτε, έγινε παραβίαση αυτών των Νόμων

τότε δεν καταρρέουν μόνο οι Νόμοι αυτοί

αλλά καταρρέει όλο το Οικοδόμημα της υπάρχουσας Φυσικής

ως "domino από τραπουλόχαρτα"

(εφόσον θεμελιώνεται, ακριβώς, στηριζόμενο σε αυτούς).

Όμως.... υπάρχουν και οι Θρησκείες που εμπεριέχουν

π.χ. θαύματα με "πολλαπλασιασμό άρτων εκ του μηδενός".

Πολλαπλασιασμός άρτων
εκ του μηδενός
στο θαύμα της Κανά
-----
«Λαβών τους πέντε άρτους και τους δύο ιχθύας,
αναβλέψας εις τον ουρανόν
ευλόγησε και κλάσας έδωκε
τοις μαθηταίς τους άρτους, οι δε μαθηταί τοις όχλοις.
και έφαγον πάντες και εχορτάσθησαν,
και ήραν το περισσεύον των κλασμάτων
δώδεκα κοφίνους πλήρεις».
(Ματθ. ι δ , 19 - 20)

------
Εδώ πρέπει να ξεκαθαριστεί ότι
τα προλεχθέντα δεν ακυρώνουν την πιθανότητα να συνέβη το παραπάνω θαύμα

Αυτό που ακυρώνεται ξεκάθαρα είναι
ότι δεν μπορεί κάποιος "να πατά σε δύο βάρκες"
δηλ.
- ή δέχεσαι θαύματα "τύπου Κανά", ως αληθή
και ελπίζεις στην βαθύτερη ύπαρξη μίας άλλης Φυσικής
που θα τα συμπεριλαμβάνει
- ή απορρίπτεις τα θαύματα "τύπου Κανά", ως ψευδή
και κατεδαφίζεις όλο το θρησκειακό οικοδόμημα
καθώς αίρεται η Πίστη.

------------

Ας δούμε, τώρα λοιπόν,

το τρόπο διαμόρφωσης των Νόμων Διατήρησης

Πρώτα, ο νόμος που διατηρεί την "ποσότητα Ηλεκτρομαγνητισμού"

σε Χωροπεριοχές

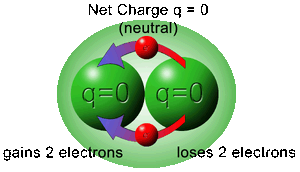Διατήρηση Ηλεκτρομαγνητισμού
σε μία Χωροπεριοχή
----
Τα φορτισμένα σωματίδια
που απαρτίζουν την οντότητα "Ηλεκτρικό Φορτίο"
(π.χ. ακίνητα ηλεκτρόνια)
που υπάρχουν σε μία Χωροπεριοχή μπορούν
να δημιουργούνται ή να καταστρέφονται
(αν το Κενό θεωρηθεί κβαντικό)
αλλά χωρίς έλλειμμα ή πλεόνασμα
Η διαφορά τους θα είναι πάντοτε μηδενική

Δεύτερο, ο νόμος που διατηρεί την "ποσότητα Ηλεκτρομαγνητισμού"

σε Κυλινδροειδείς Επιφάνειες

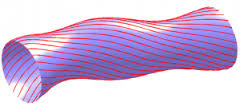Διατήρηση Ηλεκτρομαγνητισμού
σε Κυλινδροειδή Επιφάνεια
----
Τα φορτισμένα σωματίδια
που απαρτίζουν την οντότητα "Ηλεκτρικό Ρεύμα"
(π.χ. κινούμενα ηλεκτρόνια)
που διέρρευσαν καταμήκος μίας Κυλινδροειδής Επιφάνειας
έχουν μηδενικό άθροισμα (δηλ. έλλειμμα ή πλεόνασμα)
(δηλ. όσα "εισέρρευαν" από την αρχική τομή
τόσα "εξέρρευσαν" από την τελική).

Τρίτο, ο νόμος που διατηρεί την "ποσότητα Ηλεκτρομαγνητισμού"

σε Ανοικτές Επιφάνειες

Διατήρηση Ηλεκτρομαγνητισμού
σε Ανοικτή Επιφάνεια
----
Τα πεδιακά σωματίδια
που απαρτίζουν την οντότητα "Μαγνητικό Πεδίο"
(π.χ. "ακίνητα" φωτόνια)
που "τέμνονται" από μία Ανοικτή Επιφάνεια
έχουν μηδενικό άθροισμα (δηλ. έλλειμα ή πλεόνασμα)
(δηλ. όσα έχουν την τάση να "εισρεύσουν"
τόσα έχουν την τάση να "εκρεύσουν")
----
Με απλά λόγια
αν υπάρχει μια μεγάλη ροή ανθρώπων
και σε μια πόρτα χωρούν τρείς άνθρωποι να μπουν
τότε τρεις και θα βγουν

Τέταρτο, ο νόμος που διατηρεί την "ποσότητα Ηλεκτρομαγνητισμού"

σε Ανοικτές Καμπύλες

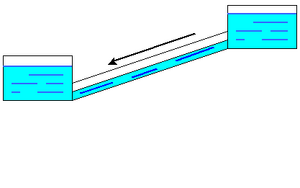Τα πεδιακά σωματίδια
που απαρτίζουν την οντότητα "Ηλεκτρικό Πεδίο"
(π.χ. κινούμενα φωτόνια)
που διέρρευσαν καταμήκος μίας Ανοικτής Καμπύλης
(στην εικόνα, ο "ευθύγραμμος σωλήνας")
έχουν μηδενικό άθροισμα (δηλ. έλλειμμα ή πλεόνασμα)
δηλ.
όσα εισήλθαν στο αρχικό σημείο
τόσα εξήλθαν στο τελικό.

----

ΣΗΜΕΙΩΣΗ:

Ο "διαβασμένος" αναγνώστης θα απορεί επειδή

ενώ οι μετρήσεις των Παρατηρητών αναφέρονται στο Παρόν

ωστόσο χρησιμοποιούνται, στα ρήματα, όχι Ενεστώτες αλλά Αόριστοι.

Αυτό συμβαίνει καθόσον στον Τρισδιάστατο (3D) Χώρο που αναφερόμαστε

όλες οι μετρήσεις "αρχίζουν" και "ολοκληρώνονται" στο Παρόν.

Δεν υπάρχει η έννοια του Χρόνου αλλά μόνον του Χώρου.

Κάποιος τώρα θα αναρωτηθεί πως νοούνται Ροή και Ρύση (δηλ. κινήσεις)

στον 3D-Χώρο (χωρίς ύπαρξη Χρόνου).

Εδώ υπενθυμίζουμε ότι, στον 3D-Χώρο, η Κίνηση υπάρχει μεν

αλλά συντελείται ακαριαία (όπως κινείται το φως στην Κλασσική Φυσική)

Ουσιαστικά, θεωρούμε ότι όλα συμβαίνουν στο "Τετελεσμένο Παρόν"

(μία διευρυμένη εννοιολογική έκφραση του Παρόντος)

χωρίς ύπαρξη Παρελθόντος και Μέλλοντος

Όπως είδαμε και προηγουμένως, η "ψυχή" και των Νόμων Διατήρησης

(που επωμίζεται το βάρος της μετατροπής)

είναι οι Τελεστές.

Πάντοτε πρέπει να θυμόμαστε ότι
ο Τελεστής είναι απλά
ένας μηχανισμός μετατροπής
ενός Φυσικού Μεγέθους (ή Γεωμετρικού ή Αλγεβρικού)
σε κάποιο άλλο Μέγεθος

Ψάχνουμε, λοιπόν, τελεστές

που θα "μηδενοποιούν" Φυσικά Μεγέθη (δηλ. που ως γνωστόν είναι συναρτήσεις)

Αυτοί, με απλά λόγια,

παίρνουν τα Φυσικά Μεγέθη

και τα μετατρέπουν

σε μηδενικά.

Εδώ οι Παρατηρητές, ανάλογα με τις θεάσεις τους, διαφοροποιούνται

- Για τον "Μακροσκοπικό" Παρατηρητή (της Μακροσκοπικής Θέσης)

κατάλληλος τελεστής είναι:

ο Κλειστός Αθροιστικός Τελεστής (Κλειστή Άθροιση)

(ή απλά, άθροισμα θετικών και αρνητικών)

- Όμως, για τον "Μικροσκοπικό" Παρατηρητή (της Μικροσκοπικής Θέσης)

υπάρχουν δύο ισοδύναμες επιλογές

α) οι Κλειστοί Ολοκληρωτικοί Τελεστές

(επιχώριος, επιφανειακός, επικαμπύλιος)

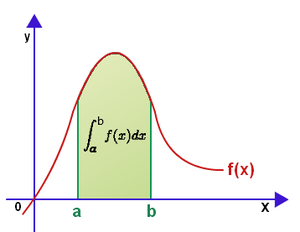Στον Τελεστή της Κλειστής Ολοκλήρωσης
τα άκρα a και b
συμπίπτουν κατ τα δύο στο μηδέν
ένα Φυσικό Μέγεθος
(στο σχήμα απεικονίζεται από την "ερυθρή" συνάρτηση)
σε
μία Γραμμή
(στο σχήμα θα απεικονιζόταν
από μία "πράσινη" ευθεία επί του άξονα y)

β) οι Διαφορικοί Τελεστές
(απόκλιση (div), στροβιλισμός (curl))

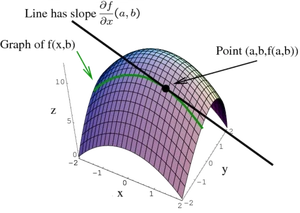Είναι δύσκολο να παρασταθούν
και να εξηγηθούν οι Διαφορικοί Τελεστές
παραστατικά
Πάντως, χοντρικά, κάνουν ακριβώς το αντίθετο
από τους "Ολοκληρωτικούς"
Δηλαδή δεν "ντύνουν" (γεωμετρικά)
αλλά "ξεντύνουν"

Ακολουθούν, λοιπόν και πάλι, οι πίνακες

που θα "αρχειοθετήσουν" τους Φυσικούς Νόμους Διατήρησης "σε κουτιά"

(όπως έγινε με τους Φυσικούς Νόμους Σύνδεσης στο προηγούμενο Μέρος)

Πρώτα, παρουσιάζεται ο πίνακας που περιλαμβάνει

τους Νόμους Διατήρησης από την σκοπιά της Μακροσκοπικής Θέασης

(δηλ. αυτών που περιγράφουν την Φυσική Οντότητα ολιστικά, ως όλον)

Εκτατική Θέαση

Γεωμετροποίηση Ηλεκτροφυσικής Ηλεκτροφυσικοί Νόμοι Διατήρησης (Πίνακας 3) Εξισώσεις A.09, A.10, A.11, A.12 (3D-Χώρος) Εκτατική Θέαση (Εκτατικά Μεγέθη) Δυναμική Άποψη (Δυναμικά Μεγέθη)
α/α	Φυσική Οντότητα & αντίστοιχη Γεωμετρική	Φυσικός Νόμος & επισυναπτόμενη Εξίσωση
A.09	Ηλεκτρικό Φορτίο (Electric Charge) Χωροπεριοχή	Νόμος Διατήρησης Ηλεκτρικού Φορτίου Σ ⋅ Ψ Q ≡ 0
A.10	Ηλεκτρικό Ρεύμα (Electric Current) Κυλινδροειδής Επιφάνεια	Νόμος Διατήρησης Ηλεκτρικού Ρεύματος Σ ⋅ Φ J = 0
A.11	Μαγνητικό Πεδίο (Magnetic Field) Ανοικτή Επιφάνεια	Νόμος Διατήρησης Μαγνητικού Πεδίου Σ⋅Φ B = 0
A.12	Ηλεκτρικό Πεδίο (Electric Field) Ανοικτή Καμπύλη	Νόμος Διατήρησης Ηλεκτρικού Πεδίου Σ∧ΓE = 0
Εμπλεκόμενα Φυσικά Μεγέθη
Φορτιακή Ολότητα (Charge Totality) (Ψ_Q) Ρευματική Ροή (Current Flux) (Φ_J) Μαγνητική Ροή (Magnetic Flux) (Φ_B) Ηλεκτρική Ρύση (Electric Flow) (Γ_E)
Εμπλεκόμενοι Τελεστές
Επιχώρια Άθροιση (Volume Summation) Επιφανειακή Άθροιση (Surface Summation) Επικαμπύλια Άθροιση (Curve Summation)		Σ⋅ Σ⋅ Σ∧

Εντατική Θέαση (Ολοκληρωτική Έκφραση)

Γεωμετροποίηση Ηλεκτροφυσικής Ηλεκτροφυσικοί Νόμοι Διατήρησης (Πίνακας 4) Εξισώσεις A.13, A.14, A.15, A.16 (3D-Χώρος) Εντατική Θέαση (Ολοκληρωτική Έκφραση) (Εντατικά Μεγέθη) Δυναμική Άποψη (Δυναμικά Μεγέθη)
α/α	Φυσική Οντότητα & αντίστοιχη Γεωμετρική	Φυσικός Νόμος & επισυναπτόμενη Εξίσωση
A.13	Ηλεκτρικό Φορτίο (Electric Charge) Χωροπεριοχή	Νόμος Διατήρησης Ηλεκτρικού Φορτίου ∰d V⋅Q≡ 0
A.14	Ηλεκτρικό Ρεύμα (Electric Current) Κυλινδροειδής Επιφάνεια	Νόμος Διατήρησης Ηλεκτρικού Ρεύματος ∯d S⃗ ⋅ J⃗ = 0
A.15	Μαγνητικό Πεδίο (Magnetic Field) Ανοικτή Επιφάνεια	Νόμος Διατήρησης Μαγνητικού Πεδίου ∯d S⃗ ⋅ B⃗ = 0
A.16	Ηλεκτρικό Πεδίο (Electric Field) Ανοικτή Καμπύλη	Νόμος Διατήρησης Ηλεκτρικού Πεδίου ∮d r⃗ ⋅ E⃗ = 0
Εμπλεκόμενα Φυσικά Μεγέθη
Φορτιακή Πυκνότητα (Charge Density) (Q) Ρευματική Πυκνότητα (Current Density) (J) Μαγνητική Ένταση (Magnetic Strength) (B) Ηλεκτρική Ένταση (Electric Strength) (E)
Εμπλεκόμενοι Τελεστές
Κλειστή Επιχώρια Ολοκλήρωση (Volume Integral) Κλειστή Επιφανειακή Ολοκλήρωση (Surface Integral) Κλειστή Επικαμπύλια Ολοκλήρωση (Curve Integral)		∰d V⋅ ∯d S⃗ ⋅ ∮d r⃗ ⋅

Εντατική Θέαση (Διαφορική Έκφραση)

Γεωμετροποίηση Ηλεκτροφυσικής Ηλεκτροφυσικοί Νόμοι Διατήρησης (Πίνακας 5) Εξισώσεις A.17, A.18, A.19, A.20 (3D-Χώρος) Εντατική Θέαση (Διαφορική Έκφραση) (Εντατικά Μεγέθη) Δυναμική Άποψη (Δυναμικά Μεγέθη)
α/α	Φυσική Οντότητα & αντίστοιχη Γεωμετρική	Φυσικός Νόμος & επισυναπτόμενη Εξίσωση
A.17	Ηλεκτρικό Φορτίο (Electric Charge) Χωροπεριοχή	Νόμος Διατήρησης Ηλεκτρικού Φορτίου Δ ⋅ Q ≡ 0
A.18	Ηλεκτρικό Ρεύμα (Electric Current) Κυλινδροειδής Επιφάνεια	Νόμος Διατήρησης Ηλεκτρικού Ρεύματος ∇⃗ ⋅ J⃗ = 0
A.19	Μαγνητικό Πεδίο (Magnetic Field) Ανοικτή Επιφάνεια	Νόμος Διατήρησης Μαγνητικού Πεδίου ∇⃗ ⋅ B⃗ = 0
A.20	Ηλεκτρικό Πεδίο (Electric Field) Ανοικτή Καμπύλη	Νόμος Διατήρησης Ηλεκτρικού Πεδίου ∇⃗ × E⃗ = 0⃗
Εμπλεκόμενα Φυσικά Μεγέθη
Φορτιακή Πυκνότητα (Charge Density) (Q) Ρευματική Πυκνότητα (Current Density) (J) Μαγνητική Ένταση (Magnetic Strength) (B) Ηλεκτρική Ένταση (Electric Strength) (E)
Εμπλεκόμενοι Τελεστές
Διαφορά (Difference) Απόκλιση (Divergence) Στροβιλισμός (Curlation)		Δ⋅ ∇⃗ ⋅ ∇⃗ ×

-----

Συμπέρασμα:

Ετσι καταλήξαμε λοιπόν, ξεκάθαρα,
σε 4 + (4x2) = 12 Νόμους Διατήρησης
που απαιτούνται για την μελέτη του Ηλεκτρομαγνητισμού.

Επιμύθιο:
------------
Αυτό που έχει νόημα να συγκρατήσει κάποιος από όλα αυτά
είναι, ουσιαστικά, όλοι αυτοί οι Φυσικοί Νόμοι είναι μόνον 4
δηλ. ότι δεν δημιουργείται ούτε καταστρέφεται Ηλεκτρομαγνητισμός
σε Χωροπεριοχές, Επιφάνειες (και των δύο ειδών) και Καμπύλες.

Περισσότερο ουσιαστικά, ο νόμος είναι ένας
δηλ. δεν δημιουργείται ούτε καταστρέφεται Υλοενέργεια
σε κανένα σημείο του Σύμπαντος, σε καμία χρονική στιγμή.

Με πιο απλά λόγια:
"Δεν μετατρέπεται, ποτέ και πουθενά, το Κάτι στο Τίποτα (και αντιστρόφως)"

Και ακόμη πιο απλοϊκά, για την Φυσική:

"Δεν μπορούν να συμβούν ούτε θαύματα της Κανά

αλλά ούτε να φυτρώσουν λεφτόδεντρα"