4D-Ηλεκτροστατική
(Μέρος 02)
Φυσικοί Νόμοι

-------------------------------------------------
ΠΕΡΙΕΧΟΜΕΝΑ ΑΥΤΗΣ ΤΗΣ ΣΕΙΡΑΣ
-------------------------------------------------

A. Συνοψίζοντας την Κλασσική Ηλεκτροστατική
είχαμε δεί ότι
αν δεν λάβουμε υπ' όψη την ύπαρξη του Χρόνου
(δηλ. θεωρούμε ως βάση
την Γεωμετρία του τρισδιάστατου (3D) Ευκλείδειου Χώρου)
τότε
η Φυσική του Ηλεκτρομαγνητισμού
περιλαμβάνει 4 Φυσικές Οντότητες
(που είναι όλες ανεξάρτητες μεταξύ τους)
που η συμπεριφορά τους καθορίζεται
από μία τετράδα Φυσικών Νόμων
....
ΣΗΜ: Υπάρχουν αρκετές τέτοιες τετράδες Φυσικών Νόμων
που όμως είναι ισοδύναμες μεταξύ τους
οπότε αρκούμαστε στις απλούστερες
που αποδίδονται στον παρακάτω πίνακα.

Παρατηρούμε ότι
τα δεύτερα μέλη των εξισώσεων
των Φυσικών Νόμων
είναι όλα μηδενικά.

Αν θέλουμε να δούμε, γραφικά,
τι σημαίνουν αυτές οι εξισώσεις
τότε
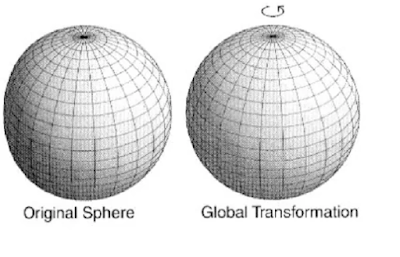
βλέπουμε το παρακάτω σχήμα
Πρέπει να φανταστούμε ότι ο τρισδιάστατος Χώρος μας
είναι καμπύλος
και αντιπροσωπεύεται από την επιφάνεια μιας σφαίρας (όχι το εσωτερικό της)
Ένας μετασχηματισμός (π.χ. μία περιστροφή)
δεν αλλοιώνει το "δικτύωμα"
(δηλ την μορφή των νοητών γραμμών που δημιουργεί
η κάθε Φυσική Οντότητα στον Χώρο)

Αυτό το γεγονός
προσδίδει στον Χώρο μία "αρμονία"
που στην Φυσική χαρακτηρίζεται ως "Global gauge symmetry"

Κάθε Φυσική Οντότητα
όταν καλύψει έναν Χώρο
(π.χ. την επιφάνεια μιας σφαίρας)
την "γραμμώνει"
(δηλ. δημιουργεί σε αυτόν, ένα νοητό δίκτυο
από Δυναμικές και Ισοσταθμικές γραμμές)
Εφόσον, τώρα,
δεν υπάρχουν χρονικές μεταβολές
αν η σφαίρα υποστεί έναν μετασχηματισμό
π.χ. μία Περιστροφή
οι γραμμές παραμένουν αναλλοίωτες

Αν θέλουμε να φέρουμε
ένα αντίστοιχο παράδειγμα από την Μαθηματική Ανάλυση
μπορούμε να αντιστοιχίσουμε την Εκθετική Συνάρτηση
Δηλαδή,
αν η φάση (x) (δηλ. o εκθέτης) είναι ίδιος με την μεταβλητή (x)
(όπου εδώ, η μεταβλητή αντιπροσωπεύει κάθε μία από τις τρείς Διαστάσεις)
τότε η παραγώγιση
αφήνει αναλλοίωτη την Εκθετική Συνάρτηση

================
B. Συνοψίζοντας
την Κλασσική Ηλεκτροδυναμική
είχαμε δεί ότι
αν λάβουμε υπ' όψη την ύπαρξη του Χρόνου
(ως μία παράμετρο, όχι ως μία επιπλέον Διάσταση)
(δηλ. συνεχίζουμε να θεωρούμε ως βάση
την Γεωμετρία του τρισδιάστατου (3D) Ευκλείδειου Χώρου)
τότε
η Φυσική του Ηλεκτρομαγνητισμού
περιλαμβάνει 4 Φυσικές Οντότητες
(που όμως δεν όλες ανεξάρτητες μεταξύ τους)
που η συμπεριφορά τους καθορίζεται και πάλι
από μία τετράδα Φυσικών Νόμων
που δείχνει ο παρακάτω πίνακας

Παρατηρούμε ότι
τα δεύτερα μέλη των εξισώσεων
των Φυσικών Νόμων
ΔΕΝ είναι όλα μηδενικά.

Αν θέλουμε να δούμε, γραφικά,
τι σημαίνουν αυτές οι εξισώσεις
τότε
βλέπουμε το παρακάτω σχήμα
Πρέπει, πάλι, να φανταστούμε ότι ο τρισδιάστατος Χώρος μας
είναι καμπύλος
και αντιπροσωπεύεται από την επιφάνεια μιας σφαίρας (όχι το εσωτερικό της)
Τώρα,
ένας μετασχηματισμός (π.χ. μία περιστροφή)
θα αλλοιώνει το "δικτύωμα"
(δηλ την μορφή των νοητών γραμμών που δημιουργεί
η κάθε Φυσική Οντότητα στον Χώρο)

Αυτό το γεγονός
προσδίδει στον Χώρο μία "δυσαρμονία"
που στην Φυσική χαρακτηρίζεται ως "Local gauge symmetry"

Εφόσον, τώρα,
υπάρχουν χρονικές μεταβολές
τότε
αν η σφαίρα υποστεί έναν μετασχηματισμό
π.χ. μία Περιστροφή
οι γραμμές δεν θα παραμείνουν αναλλοίωτες
αλλά θα αλλοιωθούν μεν
χωρίς, όμως, να χαθεί το μοτίβο τους

Αν θέλουμε να φέρουμε
το αντίστοιχο παράδειγμα από την Μαθηματική Ανάλυση
μπορούμε να αντιστοιχίσουμε, πάλι, την Εκθετική Συνάρτηση
Δηλαδή,
αν η φάση f(x) (δηλ. o εκθέτης) εξαρτάται από
(χωρίς να ταυτίζεται όπως πριν) με την μεταβλητή (x)
τότε η παραγώγιση
ΔΕΝ αφήνει αναλλοίωτη την Εκθετική Συνάρτηση

===========================================
Γ. Προχωρώντας τώρα
στην Σχετικιστική Ηλεκτροστατική
πρέπει να λάβουμε υπ' όψη την ύπαρξη του Χρόνου
ενσωματωμένου στον ευρύτερο Χωροχρόνο
(επομένως ως μία επιπλέον Διάσταση πλέον και όχι ως απλή παράμετρο)
(δηλ. θεωρούμε ως βάση
την Γεωμετρία του τετραδιάστατου (4D) Χώρου Minkowski)
οπότε τώρα
η Φυσική του Ηλεκτρομαγνητισμού
περιλαμβάνει μόνον δύο Φυσικές Οντότητες
(που είναι ανεξάρτητες μεταξύ τους)
και που η συμπεριφορά τους καθορίζεται
από μία δυάδα Φυσικών Νόμων

Παρατηρούμε ότι
και πάλι
τα δεύτερα μέλη των εξισώσεων
των Φυσικών Νόμων
είναι όλα μηδενικά.

Αν θέλουμε να δούμε, γραφικά,
τι σημαίνουν αυτές οι εξισώσεις
τότε
βλέπουμε το παρακάτω σχήμα
Πρέπει, πάλι, να φανταστούμε ότι ο τετραδιάστατος (πλέον) Χώρος μας
είναι καμπύλος
και αντιπροσωπεύεται από την επιφάνεια μιας σφαίρας (όχι το εσωτερικό της)
Τώρα,
ένας μετασχηματισμός (π.χ. μία περιστροφή)
ΔΕΝ αλλοιώνει το "δικτύωμα"
(δηλ την μορφή των νοητών γραμμών που δημιουργεί
η κάθε Φυσική Οντότητα στον Χώρο)

Αυτό το γεγονός
προσδίδει στον Χώρο μία επανόρθωση της αρχικής "αρμονίας"
που στην Φυσική χαρακτηρίζεται ως και πριν, "Global gauge symmetry"

Εφόσον, τώρα,
ο Χρόνος έχει ενταχθεί
στον Τετραδιάστατο Χωρόχρονο
οι χρονικές μεταβολές
δεν αλλοιώνουν πλέον το "δικτύωμα"
Οπότε,
αν η σφαίρα υποστεί έναν μετασχηματισμό
π.χ. μία Περιστροφή
οι γραμμές των τετραδιάστατων Φυσικών Οντοτήτων
παραμένουν αναλλοίωτες

Τέλος
στο αντίστοιχο παράδειγμα από την Μαθηματική Ανάλυση
με την αντιστοιχία της Εκθετικής Συνάρτησης
ξαναπαίρνει την αρχική του μορφή
Δηλαδή, η φάση (x) (δηλ. o εκθέτης) είναι ίδια με την μεταβλητή (x)
(πλέον, η μεταβλητή αντιπροσωπεύει κάθε μία από τις τέσσερεις Διαστάσεις)
οπότε η παραγώγιση
αφήνει αναλλοίωτη την Εκθετική Συνάρτηση

---------------------
ΣΥΜΠΛΗΡΩΜΑ
---------------------
Για όποιον ενδιαφέρεται να ξαναδει
τις ονομασίες των φυσικών μεγεθών
που εμφανίζονται στους παραπάνω Φυσικούς Νόμους
ξαναβάζουμε τους σχετικούς πίνακες
για να μην ψάχνει στα προηγούμενα.

α) Για τα Τρισδιάστατα Φυσικά Μεγέθη